- #1
TerryW
Gold Member
- 211
- 17
- Homework Statement
- The problem is MTW Exercise 21.10 (attached)
- Relevant Equations
- The relevant equation is the Initial Value equation 21.127 (attached)
Can anyone help me get started with this problem?
What should I use for Gni?
I've tried to produce Tni by working out Rni (using methods developed in an earlier chapter) but the results don't lead me anywhere.
I'm really stuck for a way forward on this problem so if anyone can help, it would be much appreciated.TerryW

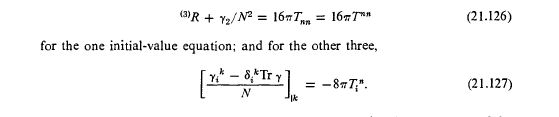
What should I use for Gni?
I've tried to produce Tni by working out Rni (using methods developed in an earlier chapter) but the results don't lead me anywhere.
I'm really stuck for a way forward on this problem so if anyone can help, it would be much appreciated.TerryW