A problem about differentiability

[rasi]

i tried to solve this problem. i can do it a little. but i can't progress. as far as I'm concerned, it requires outstanding performance. thanks for now...
PROBLEM

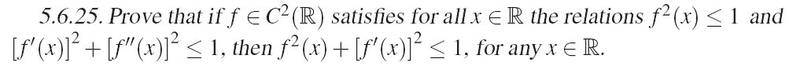
MY SOLUTION...

 

[Office_Shredder]

This is pretty tricky (unless I missed something clever). Think about this geometrically: we know that f(x) is oscillating between -1 and 1 in some fashion. The statement
$$f'(x)^2+f''(x)^2 \leq 1$$
says that the derivative of f and the second derivative cannot both be big at the same time. So for example if f'(x) is big when f(x) is near 1, it won't be able to decrease fast enough (because f''(x) is small) to prevent f(x) from crossing the value of 1, which gives a contradiction.

The question then is how to put this into something more rigorous. Suppose we're at a point a for which f(a)²+f'(a)²>1. The picture you should have in your head (not something you should assume but something to give you an idea of wha's going on) is f(a) and f'(a) both positive. Then f is going to eventually reach the value of 1 unless f'(x) decreases and is eventually 0. So the question that you need to answer: how fast can f'(x) decrease to reach 0, given that f'(x)²+f''(x)²<1?

 

[Mark44]

Mod note: This is obviously not a precalc problem, so moving it to the Calculus & Beyond section.