A problem in this photoelectric effect experiment

In summary, the photoelectric effect experiment faces a key problem related to the inconsistency of observed results when varying light frequencies and intensities. This discrepancy can lead to misinterpretations of the fundamental principles of quantum mechanics, highlighting the need for precise measurement techniques and a deeper understanding of the underlying phenomena.
  • #1
JACKR
13
1
Homework Statement
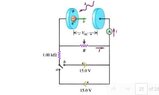
The work function of material examined using apparatus shown schematically in Fig: P38. The ammeter measures the photocurrent. The voltage of the anode relative to the cathode is VAC. The switch is in position while radiation with wavelength 140 nm is incident on the cathode. (a) The potentiometer is set at R = 3.20 kΩ and there is a photocurrent. What is the potential difference VAC? (b) The resistance is slowly adjusted to lower values until the first hint of photocurrent is detected in the ammeter. That happens when R = 334 Ω. What is the value of VAC at that point? (c) What is the work function of the cathode material? (d) The switch is then thrown to position a and the ammeter measures a photocurrent of 3.71 mA. What is the current I in this case? (e) What is the value of VAC? (f) The switch is returned to position a and the wavelength of the light is reduced to 65.0 nm. The photocurrent increases. What is the minimum value of R for which the photocurrent will cease?
Relevant Equations
e|V_AB|=hυ-φ
(a) is easy. No i. Therefore, the 1kΩ resistor and the 3.20kΩ one are connected in series. So 'I' can be easily determined and so is VAC

(b) is the same as (a)

(c) The work function should be solved for via the equation eV₀=hυ-φ, where V₀ is the absolute value for VAC from part (b)

(d) I am stuck at this. The current in the cathode-anode branch is constant regardless of the battery voltage. So, it occured to me that I should place a current source in the top branch giving 3.71 mA. The |voltage difference| between the cathode and the anode equals to IR. I thought about applying KVL in the upper loop, but when I carried this out, I didn't reach to anything.


(e) Is easy to figure out once 'I' from (d) is known

(f) given the wavelength and the figured work function, I can calculate V₀, then through applying KVL to the down loop, I will be able to determine the value of 'I' therefore, the value of R.



. . ..
 

Attachments

  • IMG_20240528_082734.jpg
    IMG_20240528_082734.jpg
    15.6 KB · Views: 22
Physics news on Phys.org
  • #2
Hi. Welcome to PF! A few comments...

JACKR said:
Homework Statement: ..... The voltage of the anode relative to the cathode is VAC. The switch is in position while radiation with wavelength 140 nm is incident on the cathode.
But the value of 'position' is missing! Presumably position b?

JACKR said:
(a) The potentiometer is set at R = 3.20 kΩ and there is a photocurrent.
But your anwer to part (a) says the photocurrent is zero - which conflicts with the information in the question.

You give the equation "e|V_AB|=hυ-φ". I would use ##V_S## (stopping potential) in the equation. And the modulus (absolute value) symbol suggests the polarity of the voltage does not matter - but it does. A more conventional form of the the equation is therefore ##eV_S = h\nu - \phi##.

You could improve the readability of the Homework Statement a lot by starting each question in a new paragraph. Much easier on our eyes – so you’re more likely to get replies!
 
  • Like
Likes JACKR and nasu
  • #3
But to actually answer your question...

JACKR said:
(d) I am stuck at this. The current in the cathode-anode branch is constant regardless of the battery voltage. So, it occured to me that I should place a current source in the top branch giving 3.71 mA. The |voltage difference| between the cathode and the anode equals to IR. I thought about applying KVL in the upper loop, but when I carried this out, I didn't reach to anything.
I is the current through the variable resistor (presumably still set at 334 Ω).
What is the current through the battery in terms of I and i?
What is the current through the fixed resistor in terms of I an i?

Then consider the loop containing only the battery and two resistors.
 
  • Like
Likes JACKR
  • #4
But why would you assume that it's still set at 334 Ω?
 
  • #5
JACKR said:
But why would you assume that it's still set at 334 Ω?
Because 334 Ω is the last value given for R (in part (b)) and the question tells you when R is changed. And, as far as I can see, you need the value of R to answer question-parts (d) and (e).

Any comments on what I said in Post #2 by the way?
 
  • #6
Regarding part (b), you can think of it as the moment just before the one moment when current flows. Indeed, this is only way to solve the problem. Also, the value calculated there is the value of the stoping potential. About the equation, I think you're right. I shouldn't have put a modulus around VAC. Thank you for your help.
 
  • #7
(a) The potentiometer is set at R = 3.20 kΩ and there is a NO photocurrent. What is the potential difference VAC?
It's a a typo in the statement of the question.
 
  • #8
JACKR said:
(a) The potentiometer is set at R = 3.20 kΩ and there is a NO photocurrent. What is the potential difference VAC?
It's a a typo in the statement of the question.
Yes. The other typo's I can spot are also important:
________________________

"The switch is in position while radiation with wavelength 140 nm is incident ..."
should be
"The switch is in position b while radiation with wavelength 140 nm is incident ..."
________________________

"(f) The switch is returned to position a ..."
should be
"(f) The switch is returned to position b ..."
________________________

Hope you managed parts (e) and (f). Post again if you still need help.

Edited.
 
  • Like
Likes JACKR
  • #9
Steve4Physics said:
Yes. The other typo's I can spot are also important:
________________________

"The switch is in position while radiation with wavelength 140 nm is incident ..."
should be
"The switch is in position b while radiation with wavelength 140 nm is incident ..."
________________________

"(f) The switch is returned to position a ..."
should be
"(f) The switch is returned to position b ..."
________________________

Hope you managed parts (e) and (f). Post again if you still need help.

Edited.
Thanks for pointing them out. Yeah, I managed parts (e) and (f); thank you!
 
  • Like
Likes Steve4Physics

FAQ: A problem in this photoelectric effect experiment

What is the photoelectric effect?

The photoelectric effect is the phenomenon where electrons are emitted from a material, typically a metal, when it is exposed to light or electromagnetic radiation of sufficient energy. This effect demonstrates the particle nature of light and is a key concept in quantum mechanics.

What are some common problems encountered in photoelectric effect experiments?

Common problems include insufficient light intensity, improper wavelength of light used, equipment calibration issues, and external factors such as temperature and environmental noise that can affect measurements. Additionally, the quality of the photoemissive material can significantly impact results.

How can I ensure accurate measurements in a photoelectric effect experiment?

To ensure accurate measurements, use a monochromatic light source with a known wavelength, calibrate your equipment before experiments, minimize external light interference, and maintain a controlled environment. Additionally, repeat measurements to account for variability and average the results for better accuracy.

What role does the work function play in the photoelectric effect?

The work function is the minimum energy required to remove an electron from the surface of a material. If the energy of the incoming photons (light) exceeds the work function, electrons will be emitted. If it does not, no electrons will be emitted, regardless of the intensity of the light.

Why is the photoelectric effect important in modern technology?

The photoelectric effect is fundamental to many technologies, including solar cells, photodetectors, and photoelectric sensors. It also provides critical insights into the nature of light and matter, influencing advancements in quantum mechanics and contributing to the development of various electronic devices.

Similar threads

Two vertical bars are connected at the bottom via resistance......
Replies
7
Views
297
An experiment for the determination of hydrogen ionization energy
Replies
1
Views
1K
Photoelectric Effect Graph and Work Function Questions
Replies
25
Views
3K
Questions Regarding the Photoelectric Effect
Replies
11
Views
1K
Interpreting I-V graphs in Photoelectric effect
Replies
3
Views
4K
Releasing Electrons with a color filter
Replies
2
Views
1K
I need opinions on a Projectile Motion problem that I made up
Replies
11
Views
1K
Finding the Current in a circuit
Replies
6
Views
2K
Calculating Stopping Potential in Photoelectric Effect Experiment
Replies
4
Views
2K
Confused about derivation of E=(V-IR)/L, multiple choice problem
Replies
3
Views
4K

Hot Threads

Recent Insights

Back
Top