A problem when trying to compare electromagnetism with gravity

[Myslius]

Let's say an object far far away from the Earth free falls in gravitational field. At Earth's surface free falling object gains kinetic energy E_1.
Let's say an electron far away from the proton free falls in electromagnetic field. At Bohr's radius free falling electron gains kinetic energy E_2.
Let's say on object is standing still on the surface of the Earth and it gets an energy equal to E_1, object escapes to infinity.

Now here's the problem, that i don't get. Free falling electron gains E_2=13.6eV when distance to the nucleus is Bohr's radius * 2.
13.6 eV is energy required to strip electron from hydrogen nucleus (confirmed experimentally).
Electron gains 27.2eV at Bohr's radius. Where's this factor of 2 coming from?

Calculations come from a little simulation program that i wrote:


In the case of gravity, program integrates Newton's gravitational law.

In the case of electromagnetism program integrates coulomb's law

Everything looks fine in the case of gravity, but in the case of electromagnetism, i get an output:

V1: 3093155.3510288
V2: 1684.5850519587
A1: 9.047093214817E+22
A2: 4.9272009529973E+19
M1: 2.8176738503187E-24
M2: 2.8176738503187E-24
Total Time: 0.06977473942106
Distance: 5.290930084121E-11
Energy1: 4.3577514737836E-18, eV: 27.201084699357
Energy2: 2.3733056247709E-21, eV: 0.01481417370982

V looks fine (velocity m/s)
A looks fine (acceleration m/s^2)
M looks fine (momentum of a proton and momentum of an electron)
Energy and distance have a weird factor of 2. Why?

My initial thought was that Lorentz force is a sum of both forces between the electron and the proton, however that doesn't seem to be the case.

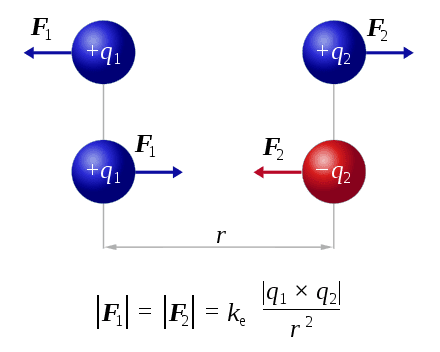
F1 is equal to F2 and is equal to k_e * q1 * q2 / (r*r)
and not
F1 + F2 = k_c * q1 * q2 / (r*r)

What is wrong here?

 

[mjc123]

You are not comparing like with like. The correct comparison for a Bohr atom would be with an object in low Earth orbit. For an orbiting object, PE = -2KE and total energy = -KE; escape energy = KE. KE of the orbiting object is half that of an object freely falling from infinity to the orbital radius. Simply dropping an object from infinity won't cause it to go into orbit; you have to lose some of that energy somehow (e.g. the proton-electron system you describe has total energy 0, while a Bohr atom has energy -13.6 eV, PE -27.2, KE +13.6).

 

[Myslius]

You are not comparing like with like. The correct comparison for a Bohr atom would be with an object in low Earth orbit. For an orbiting object, PE = -2KE and total energy = -KE; escape energy = KE. KE of the orbiting object is half that of an object freely falling from infinity to the orbital radius. Simply dropping an object from infinity won't cause it to go into orbit; you have to lose some of that energy somehow (e.g. the proton-electron system you describe has total energy 0, while a Bohr atom has energy -13.6 eV, PE -27.2, KE +13.6).

For an electron "hovering at Bohr's radius", escape energy would be E2 = 27.2 eV, but since electron can't stand still and is orbiting with E_orbital = 13.6 eV, It takes another 13.6. eV to kick electron out, if the light hits at correct angle? Is that correct? According to orbital mechanics, E1 angle is the most optimal angle to boost velocity for escape trajectory (picture below). I have a following question. How does that work with spectral lines? Spectral lines are quite narrow, electron could be in any orientation relative to the photon. And another question is about Compton scattering.

When a photon hits an electron, only small fraction of energy is transferred to the electron, this is because energy and momentum must be conserved. When a photon with 13.6 eV hits an electron, only 13.6eV/18787=0.000723eV of energy is transferred. The photon bounces with 99.99% of initial energy back.

Now, here's an interesting thought, maybe 13.6eV only looks like 13.6eV, but what would happen if E1 is actually 13.6eV*18787=0.25MeV? from the Compton formula we get, that a photon disappears, because it transfers every bit of energy on perfect collision. E_final - E_initial = electron's mass = 0.25MeV. Electron is emitted. which is not 13.6eV, and we actually see 0.5MeV (electron) outside from the nucleus. (I'm missing 2 somewhere here again, i know i need to contemplate more and to order my thoughts more precise, but if you have any insights corrections let me know)
The case that I'm talking about is when the bottom of Compton scattering formula looks like: 1 + (0.5 * (1+1)), E_final/E_initial=2, and angle is pi. It looks like h in E=hf is a quite off. I know this is far fetched, but that's what i get when i look at Compton scattering and Bohr's model. Also it looks like E1 is facing the opposite direction. I'm not sure h is off, might be c because not in vacuum, might be coulomb's constant, maybe particle masses. Any ideas? How to resolve Compton scattering in the Bohr model?