A pulley system with two pulleys and two suspended masses

[member 731016]

Homework Statement

Pls see below

Relevant Equations

Pls see below

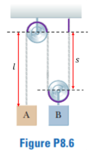
For this problem,

The solution is,

However, how do they know the block B will move up and block A will move down? The masses of each are not given so could be the other way round if $m_b > m_a$?

Also how do they know that if block B moves up by 1cm, block A will move down by 2cm?

Many thanks!

 

[kuruman]

The problem states that the masses are equal and the solution is based on that.

 

[member 731016]

The problem states that the masses are equal and the solution is based on that.

Thank you for your reply @kuruman !

Sorry I did not see that! I will try the problem again.

Many thanks!

 

[BvU]

Also how do they know that if block B moves up by 1cm, block A will move down by 2cm?

That is a matter of 'counting': in the picture you see three lengths of cord. Think of the situation that block A is all the way down: by then A has dropped by two lengths, whereas B has gone up by only one length.

$\$

 

[member 731016]

That is a matter of 'counting': in the picture you see three lengths of cord. Think of the situation that block A is all the way down: by then A has dropped by two lengths, whereas B has gone up by only one length.

$\$

Thank you for your reply @BvU!

I think I might see what you mean from intuition, is there way to prove this thought?

Many thanks!

 

[erobz]

Thank you for your reply @BvU!

I think I might see what you mean from intuition, is there way to prove this thought?

Many thanks!

Write the total length of the inextensible rope $L$, In terms of all the other lengths of each section. There will be a couple more steps, but that is where you start.

 

[BvU]

is there way to prove this thought?

Yes ! The overwhelming beauty of physics: The experiment decides !

$\$

 

[member 731016]

View attachment 322795

Write the total length of the inextensible rope $L$, In terms of all the other lengths of each section. There will be a couple more steps, but that is where you start.

Thank you for your reply @erobz ! That diagram is quite helpful :)

$L = l + s + 2.5 \times purple~semicircle$

Many thanks!

 

[member 731016]

Yes ! The overwhelming beauty of physics: The experiment decides !

$\$

Thank you for your reply @BvU!

 

[erobz]

Thank you for your reply @erobz ! That diagram is quite helpful :)

$L = l + s + 2.5 \times purple~semicircle$

Many thanks!

Sorry, I shouldn't have drawn that top section purple, it could be any length. I'll update the image.

1) just assign a random variable to each length that is not already labeled.
2) you are missing some length of rope in that sum.

 

[member 731016]

Sorry, I shouldn't have drawn that top section purple, it could be any length.

1) just assign a random variable to each length that is not already labled
2) you are missing some length of rope in that sum.

Thank you for your reply @erobz !

Is the ok for the variables?

Many thanks!

 

[member 731016]

From the diagram it looks like $c = b$, but would you like me to leave it like that @erobz ?

Many thanks!

 

[erobz]

Thank you for your reply @erobz !

Is the ok for the variables?
View attachment 322798
Many thanks!

Yeah, that will work.

 

[member 731016]

Yeah, that will work.

Thank you for your reply @erobz !

$L = a + s + b + c + l$

Many thanks!

 

[erobz]

Thank you for your reply @erobz !

$L = a + s + b + c + l$

Many thanks!

ok, but you are still missing a length of rope there.

 

[member 731016]

ok, but you are still missing a length of rope there.

Thank you for your reply @erobz !

Sorry should be $L = a + 2s + b + c + l$ and assuming that the pulleys are the same size as the rope is taut, then $c = b$ so simplifying gives $L = a + 2s + 2b + l$

Many thanks!

 

[erobz]

Thank you for your reply @erobz !

Sorry should be $L = a + 2s + b + c + l$

Many thanks!

Great! Now identify the only variables that change in that equation when the blocks move.

 

[member 731016]

Great! Now identify the only variables that change in that equation when the blocks move.

Thank you for your reply @erobz !

The variables that change are $l$ and $s$

Many thanks!

 

[member 731016]

Thank you for your reply @erobz !

The variables that change are $l$ and $s$

Many thanks!

I guess they are functions of time then?

Many thanks!

 

[erobz]

I guess they are functions of time then?

Many thanks!

Don't worry about that just yet.

So $l$ and $s$ are the only length that can change. Apply a change to each of the variables.

For instance if a varianle was $z$ we would apply a change by adding $\Delta z$ to it. etc...

Write the new equation.

 

[member 731016]

Don't worry about that just yet.

So $l$ and $s$ are the only length that can change. Apply a change to each of the variables.

For instance if a varianle was $z$ we would apply a change by adding $\Delta z$ to it. etc...

Thank you for your reply @erobz !

The change for each length is

$\Delta l$
$\Delta s$

Which in the original equation is

$L = a + 2\Delta s + 2b + \Delta l$Many thanks!

 

[erobz]

Thank you for your reply @erobz !

The change for each length is

$\Delta l$
$\Delta s$

Many thanks!

So what is the new equation? Rember a variable that changes goes from $z \to z+ \Delta z$.

 

[member 731016]

Thank you for your reply @erobz !

I this this equation,

$L = a + 2\Delta s + 2b + \Delta l$

Can also be expressed as$L_i = L_f$
$a + 2s_i + 2b + l_i = a + 2s_f + 2b + l_f$
$2s_i + l_i =2s_f+ l_f$

Many thanks!

 

[member 731016]

So what is the new equation? Rember a variable that changes goes from $z \to z+ \Delta z$.

Thank you for your reply @erobz!

Do you mean

$z_i = z_f + \Delta z$?

If you want I could edit post #23 to use that notation. This is giving me conservation of string vibes I remember sometime talking about it on Discord.

Many thanks!

 

[erobz]

Thank you for your reply @erobz!

Do you mean

$z_i = z_f + \Delta z$?

If you want I could edit post #23 to use that notation. This is giving me conservation of string vibes I remember sometime talking about it on Discord.

Many thanks!

you don't need the subscripts. Its just saying you take what was labeled $z$ in the original eq. and replace it with $z + \Delta z$.

 

[member 731016]

I think @erobz that,

$L_i = 2s_i + l_i =2s_f+ l_f = L_f$

is really just a conservation of string statement, correct?

Many thanks!

 

[member 731016]

you don't need the subscripts. Its just saying you take what was labeled $z$ in the original eq. and replace it with $z + \Delta z$.

Oh ok thank you for your reply @erobz !

I'm not too familiar with that notation. I will change to that notation.

Many thanks!

 

[erobz]

Oh ok thank you for your reply @erobz !

I'm not too familiar with that notation. I will change to that notation.

Many thanks!

I believe it's the standard we approach stuff in Calculus.

 

[member 731016]

Hi @erobz ,

Is the reason why you used arrows for this $z \to z+ \Delta z$ because if you use equal sign then

$z = z+ \Delta z$
$z = z+ z_f - z_i$
$z_i = z_f$

Oh which is conservation of the quantity z anyway!

Many thanks!

 

[member 731016]

I believe it's the standard we approach stuff in Calculus.

Oh thank you for your reply @erobz !

 

[member 731016]

Here it is @erobz ,

$L = a + 2s + \Delta 2s+ 2b + l + \Delta l$

Many thanks!

 

[erobz]

Hi @erobz ,

Is the reason why you used arrows for this $z \to z+ \Delta z$ because if you use equal sign then

$z = z+ \Delta z$
$z = z+ z_f - z_i$
$z_i = z_f$

Oh which is conservation of the quantity z anyway!

Many thanks!

Its just shorthand math notation for saying $z$ goes to $z + \Delta z$. The variable $z$ wouldn't equal $z + \Delta z$ except in the case that $\Delta z \to 0$

 

[member 731016]

Its just shorthand math notation for saying $z$ goes to $z + \Delta z$. The variable $z$ wouldn't equal $z + \Delta z$ except in the case that $\Delta z \to 0$

Thank you for your reply @erobz !

So an equivalent notation is

$z ≈ z + dz$

 

[erobz]

Here it is @erobz ,

$L = a + 2s + \Delta 2s+ 2b + l + \Delta l$

Many thanks!

Ok, now equate the two equations through the variable $L$ and cancel the terms. What are you left with?

Edit: keep the $\Delta$ next to the $s$

 

[member 731016]

Ok, now equate the two equations through the variable $L$ and cancel the terms. What are you left with?

Thank you for your reply @erobz!

Which two equations sorry?

Many thanks!

 

[erobz]

Which two equations sorry?

Many thanks!

The first one we derived with that one. they both equal $L$. You are attempting to figure out how the changes in each variable relate to each other.

 

[member 731016]

The first one we derived with that one. they both equal $L$.

Thank you for your reply @erobz !

That must be $L = a + 2s + 2b + l$ and $L = a + 2s + \Delta 2s+ 2b + l + \Delta l$

So
$a + 2s + 2b + l = a + 2s + \Delta 2s+ 2b + l + \Delta l$
$0 = \Delta 2s + \Delta l$
$-\Delta 2s = \Delta l$
$2(s_f - s_i) = l_f - l_i$
Many thanks!

 

[erobz]

Thank you for your reply @erobz !

That must be $L = a + 2s + 2b + l$ and $L = a + 2s + \Delta 2s+ 2b + l + \Delta l$

So
$a + 2s + 2b + l = a + 2s + \Delta 2s+ 2b + l + \Delta l$
$0 = \Delta 2s + \Delta l$

Many thanks!

Move one of them to the other side of the zero. And if you want to know how far pulley B moves in terms of a how far pulley A moves solve for $\Delta s$.

 

[erobz]

Again. Keep the $\Delta$ touching the $s$. They are stuck together. Joined at the hip! don't put that 2 in between them.

 

[member 731016]

Again. Keep the $\Delta$ touching the $s$. They are stuck together. Joined at the hip! don't put that 2 in between them.

Thank you for your reply!

Sorry @erobz missed that message,

$-2\Delta s = \Delta l$

Many thanks!

 

[member 731016]

Thank you for your help @erobz !

Just a side question, how were we allowed to add the $\Delta$ to $s$ and $l$ then set them equal to each other?

Many thanks!

 

[erobz]

Thank you for your help @erobz !

Just a side question, how were we allowed to add the $\Delta$ to $s$ and $l$ then set them equal to each other?

Many thanks!

Because the change is unsigned. It could be a positive change. It could be a negative change. It may appear like were adding to both lengths but is turns out we weren't. Notice the equation dictates a positive change in the variable $l$ ( $\Delta l > 0$) demands and negative change in $s$ ( $\Delta s < 0$), and visa-versa.

 

[member 731016]

Because the change is unsigned. It could be a positive change. It could be a negative change. It may appear like were adding to both lengths but is turns out we weren't. Notice the equation dictates a positive change in the variable $l$ ( $\Delta l > 0$) demands and negative change in $s$ ( $\Delta s < 0$), and visa-versa.

Thank you for your reply @erobz !

I think we can only add the $\Delta$ to the variable that is changing if know that there is a constraint for example the string length is conserved, correct?

Many thanks!

 

[erobz]

Thank you for your reply @erobz !

I think we can only add the $\Delta$ to the variable that is changing if know that there is a constraint for example the string length is conserved, correct?

Many thanks!

No. You can add it to anything. The only constraint needed is that you have a relationship between some variables. It's simply saying we have this relationship between all these variables, lets pick some or, all that can change and change them a bit from where they currently are valued at, and see how they respond to each other. How it all pans out or the end goal is specific to each situation.

The main motivation is derivatives and differential equations, where you are looking for the change in one variable w.r.t a change in another variable. You've got time to learn all this. You don't have to figure all this out yesterday.

 

[member 731016]

No. You can add it to anything. The only constraint needed is that you have a relationship between some variables. It's simply saying we have this relationship between all these variables, lets pick some or, all that can change and change them a bit from where they currently are valued at, and see how they respond to each other. How it all pans out or the end goal is specific to each situation.

The main motivation is derivatives and differential equations, where you are looking for the change in one variable w.r.t a change in another variable. You've got time to learn all this. You don't have to figure all this out yesterday.

Thank you for your help @erobz ! :)

 

[haruspex]

$L = a + 2\Delta s + 2b + \Delta l$

No, the deltas are the increases in length. The original lengths should still be in the equation. You should have just replaced $s$ with $s+\Delta s$, etc.

 

[BvU]

I am somewhat flabbergasted at the length () of this thread!
If you do the experiment with a real piece of rope things will be clear quickly.

If you still insist on a mental exercise, remove all unessentials: reduce the pulleys to points, etc

$\$

 

[erobz]

No, the deltas are the increases in length. The original lengths should still be in the equation. You should have just replaced $s$ with $s+\Delta s$, etc.

It was getting late! I guess my mind was just inserting symbols that weren’t there.

Edit: Actually at a later post (#31) than what you must have been quoting they did get the proper result.

 

[Lnewqban]

However, how do they know the block B will move up and block A will move down?
...
Also how do they know that if block B moves up by 1cm, block A will move down by 2cm?

Do you now understand how do they know those things?

If not, please see:
https://www.physicsforums.com/threa...2-dynamics-problem-involving-a-pulley.991370/

 

[member 731016]

No, the deltas are the increases in length. The original lengths should still be in the equation. You should have just replaced $s$ with $s+\Delta s$, etc.

Thank you for your reply @haruspex ! I will try that sometime.

Many thanks!