A question about angular momentum and torques....

[NoahCygnus]

There is something I don't quite understand about the law of conservation of angular momentum.

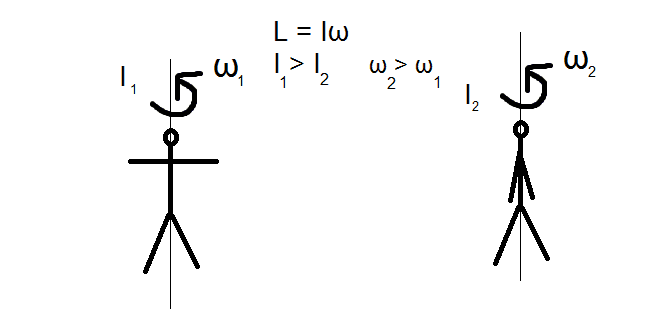
Let's say a person is rotating about an axis passing through his/her centre of mass, with an angular speed speed ω1, and has a rotational inertia I1 about about the centre of mass. No torque is acting on the person. The person lowers his arms bringing them closer to his body, lowering the rotational inertia to I2. As no torque acts on him, the angular momentum shouldn't change, so the angular speed goes up and he starts rotating faster, with an angular speed of ω2. But there is a change in angular velocity, that means there is an angular acceleration, and we know τ = Iα , so a torque should act on the person. I don't quite understand this, I would appreciate if you explain to me why there will be no torque if there is an angular acceleration on the person.

 

[jbriggs444]

we know τ = Iα

If moment of inertia is fixed, then $\tau = \frac{dL}{dt} = \frac {d(I \omega)}{dt} = I \frac{d \omega}{dt} = I\alpha$.

But if moment of inertia is not fixed then $\tau = \frac{dL}{dt} = \frac{d(I \omega)}{dt} = I \frac{d \omega}{dt} + \omega \frac{dI}{dt} = I\alpha + \omega \frac{dI}{dt}$.

 

[vanhees71]

As already in translational motion an acceleration doesn't necessarily imply the action of a force but only a change in momentum. If mass changes also the speed changes such that the momentum stays constant. Here it's the same: A torque is only necessary to change angular momentum, but here $L$ stays unchanged, i.e., $I_1 \omega_1=I_2 \omega_2$.

 

[NoahCygnus]

As already in translational motion an acceleration doesn't necessarily imply the action of a force but only a change in momentum. If mass changes also the speed changes such that the momentum stays constant. Here it's the same: A torque is only necessary to change angular momentum, but here $L$ stays unchanged, i.e., $I_1 \omega_1=I_2 \omega_2$.

In case of linear momentum, if a body's mass changes, there is a change in velocity due to internal forces, which we cancel out when we consider the entire system, that is the remaining mass and mass ejected. I can't relate that to angular momentum, I can't seem to imagine how internal torques can cause a change in angular velocity.

 

[NoahCygnus]

If moment of inertia is fixed, then $\tau = \frac{dL}{dt} = \frac {d(I \omega)}{dt} = I \frac{d \omega}{dt} = I\alpha$.

But if moment of inertia is not fixed then $\tau = \frac{dL}{dt} = \frac{d(I \omega)}{dt} = I \frac{d \omega}{dt} + \omega \frac{dI}{dt} = I\alpha + \omega \frac{dI}{dt}$.

I get it, inertial mass is also variable so we have to use the second equation. But how does that explain why there is no torque? Unless ω dI/dt = Iα , I don't understand how there will be no torque.

 

[vanhees71]

In case of linear momentum, if a body's mass changes, there is a change in velocity due to internal forces, which we cancel out when we consider the entire system, that is the remaining mass and mass ejected. I can't relate that to angular momentum, I can't seem to imagine how internal torques can cause a change in angular velocity.

Again: A torque changes angular momentum, not necessarily angular velocity. In your example there is no torque, and thus angular momentum stays constant. Since the moment of inertia around the rotation axis changes, angular velocity must change such as to keep angular momentum constant.

For a simple example with translational motion, think about a wagon filled with water, running on a horizontal track along the $x$-direction with the water flowing out (perpendicular to the plane). Then momentum is constant, which means (since the water doesn't transfer any momentum in $x$ direction)
$$\dot{m} v + m \dot{v}=0.$$
Now assume, for simplicty $\dot{m}=\mu=\text{const}$, and you get
$$\dot{v}=-\frac{\mu}{m} v.$$
So what happens (note that in the exampe $\mu<0$)?

 

[jbriggs444]

I get it, inertial mass is also variable so we have to use the second equation. But how does that explain why there is no torque? Unless ω dI/dt = Iα , I don't understand how there will be no torque.

You have a sign error there. $\omega \frac{dI}{dt} = - I \alpha$

Edit: This makes sense. If you increase angular rotation rate while holding angular momentum constant, you must be decreasing the moment of inertia.