A question about current density in finite element analysis

[JH_1870]

I know that if there is only one conductor providing the current density, then the current density can be used.

But if you apply Maxwell's equation when there are multiple current sources, I don't know which value to use.

This is not an analysis using a tool, but a problem when I develop the code myself.

Should I calculate all the values for multiple independent sources and then add them up?

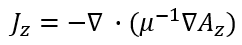
Where J is the applied current density. Is it correct to use the applied current density when calculating the magnetic potential in the iron core?

And, when there are several applied current densities, is it necessary to apply the superposition principle to solve them?

 

[Charles Link]

This appears to be a very non-trivial problem that you are trying to solve. For problems with ferromagnetic materials, sometimes the geometry involved leads to simplifying assumptions, particularly in the case of transformers. You might find some good reading in this thread, along with some of the "links" that are referenced: https://www.physicsforums.com/threads/magnetic-flux-is-the-same-if-we-apply-the-biot-savart.927681/
For the general case of magnetic materials with currents in conductors, I think it may be a very difficult problem that you are trying to tackle.

 

[Charles Link]

Just an additional comment or two: This type of problem can not be solved as a perturbation with a small response and source generated from the ferromagnetic material. Instead, in many cases, the response of the ferromagnetic material may be many and many times larger than the original source from the free currents in the conductor. Perhaps others may also comment, but this is my take on this problem.