A question about rolling motion of a wheel on a frictionless surface

[NoahCygnus]

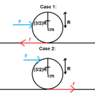
Let's imagine a situation where we have a wheel of mass $M$ and radius $R$ on a frictionless surface, and we apply a force $\vec{F}$ as shown in the diagram. The force will produce both linear acceleration of centre of mass $a$ and angular acceleration $\alpha$. The wheel starts to both translate and rotate, and we remove the external forcr. I know the condition for rolling is $v_{com} = R\omega$. The question is, most textbooks include a surface with friction , and I can't tell if without friction the above condition for rolling will be met or the wheel will slip. How can I know ?

 

[BvU]

As drawn, the wheel will slip: angular acceleration will exceed linear acceleration. If $F$ is applied below the c.o.m, the reverse. Somewhere there is a height where even without friction the rolling condition is met. What height ? A very nice exercise for someone lke you !

 

[kuruman]

The problem without friction is equivalent to a puck on a frictionless table pulled by a string wrapped around its circumference. The tension will exert a torque about the CM that will start the wheel spinning around its center and it will also accelerate the CM. Use Newton's Second law for rotation and translation to analyze the motion and answer your question.

 

[NoahCygnus]

As drawn, the wheel will slip: angular acceleration will exceed linear acceleration. If $F$ is applied below the c.o.m, the reverse. Somewhere there is a height where even without friction the rolling condition is met. What height ? A very nice exercise for someone lke you !

As drawn, the wheel will slip: angular acceleration will exceed linear acceleration. If $F$ is applied below the c.o.m, the reverse. Somewhere there is a height where even without friction the rolling condition is met. What height ? A very nice exercise for someone lke you !

If the wheel is a cylinder, and I apply the force above the centre of mass at $r$, causing a rotation about an axis passing through the cm, perpendicular the circular surfaces of the cylinder, then
$F = Ma_{cm}$
$a_{cm} = F/M$

$\tau = rF = I_{cm}\alpha$
$\alpha= \tau/I_{cm}$

The tangential acceleration of a point on the circumference will be, $a_{t} = R\alpha \Longrightarrow a_{t} = R(\tau/I_{cm}) \Longrightarrow a_{t} = R(rF/I_{cm})$

If the wheel is to roll then, $v_{cm} = v_{t} \Longrightarrow d(v_{cm})/dt = d(v_{t})/dt \Longrightarrow a_{cm} = a_{t}$
$F/M = R(rF/I_{cm}) \Longrightarrow F/M = R(rF/1/2 MR^2) \Longrightarrow 2r = R \Longrightarrow r = R/2$

So I have to apply the force at a height $R/2$, right?

And if I apply the force below the centre of mass, the wheel will slip, right?

 

[BvU]

So I have to apply the force at a height $R/2$ , right?

above the center of mass, yes. You can eliminate ambiguity by calling that a height ${3\over 2}R$

And if I apply the force below the centre of mass, the wheel will slip, right ?

Not wrong, but incomplete. How about a height in the range $R$ to ${3\over 2}R$ ?

Well done !

(the same exercise for a sphere is worked out here under 'sweet spot' )

 

[NoahCygnus]

above the center of mass, yes. You can eliminate ambiguity by calling that a height ${3\over 2}R$
Not wrong, but incomplete. How about a height in the range $R$ to ${3\over 2}R$ ?

Well done !

(the same exercise for a sphere is worked out here under 'sweet spot' )

I did the math for the range $R$ to $(3/2) R$ and found that the tangential acceleration of a point on circumference will always be greater than the linear acceleration of the centre of mass. As a result the body will skid. Can you please explain to me how friction prevents the skidding if I apply a force in that range?
Also I checked the article , it seems quite useful. I will read it once I am free.

 

[BvU]

found that the tangential acceleration of a point on circumference will always be greater than the linear acceleration of the centre of mass

You mean the tangential acceleration required for the no-slipping condition, right ?
If height = $3/2\, R\$ gives no skidding, anything below means skidding will occur to increase angular velocity, and anything above means skidding will reduce it until rolling catches up.

 

[A.T.]

Can you please explain to me how friction prevents the skidding if I apply a force in that range?

Static friction is an additional force in your equation. Assume pure rolling and then solve for the friction force required to achieve it.

 

[NoahCygnus]

You mean the tangential acceleration required for the no-slipping condition, right ?
If height = $3/2\, R\$ gives no skidding, anything below means skidding will occur to increase angular velocity, and anything above means skidding will reduce it until rolling catches up.

Yes that's what I meant.
I understand. Let's talk about the direction of frictional force. I infer that if I apply a force below $(3/2)R$ , such that skidding occurs, the direction of frictional force will be opposite to the translation motion of centre of mass, as to reduce the speed of centre of mass and to provide a negative torque to the wheel, so to increase its angular speed (Case 1 in the diagram). And if I apply the force above centre of mass, slipping will occur, so friction will act in forward direction as to speed up the centre of mass, and provide a positive torque, so to lower the angular speed until the rolling condition is met (Case 2 in the diagram). Am I correct? Also I read somewhere once the rolling condition is met, frictional force vanishes, how is that possible? I am having a hard time understanding that.

 

[BvU]

frictional force vanishes

The trajectory of a point on the circumference of the rolling object is a cycloid: at the ground it moves down and up again, so not horizontally.

 

[A.T.]

Let's talk about the direction of frictional force. I infer that if I apply a force below $(3/2)R$ , such that skidding occurs, the direction of frictional force will be opposite to the translation motion of centre of mass, as to reduce the speed of centre of mass and to provide a negative torque to the wheel, so to increase its angular speed (Case 1 in the diagram). And if I apply the force above centre of mass, slipping will occur, so friction will act in forward direction as to speed up the centre of mass, and provide a positive torque, so to lower the angular speed until the rolling condition is met (Case 2 in the diagram). Am I correct?

Yes, and the above also applies when no skidding occurs, due to sufficient static friction. The static friction has the direction that you describe above for kinetic friction, while its magnitude is whatever is required to ensure the rolling condition for linear and angular accelerations.

Also I read somewhere once the rolling condition is met, frictional force vanishes, how is that possible?

Pure rolling means no sliding, thus no kinetic friction, but you still can have static friction.

 

[NoahCygnus]

Yes, and the above also applies when no skidding occurs, due to sufficient static friction. The static friction has the direction that you describe above for kinetic friction, while its magnitude is whatever is required to ensure the rolling condition for linear and angular accelerations.

Pure rolling means no sliding, thus no kinetic friction, but you still can have static friction.

Let's talk about the energy. If the object smoothly rolls down an incline in a conservative field, such that no sliding occurs, the mechanical energy will be conserved even if there is static friction because static friction is a non-dissipative force. Am I correct?
If that's the case how come in reality, a smoothly rolling wheel loses kinetic energy?

 

[A.T.]

If that's the case how come in reality, a smoothly rolling wheel loses kinetic energy?

https://en.wikipedia.org/wiki/Rolling_resistance
https://en.wikipedia.org/wiki/Drag_(physics)