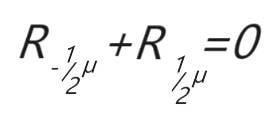A question about tensor calculus in Von Neumann algebra (W*)

[Tommolo]

TL;DR Summary

I was wondering about how to apply Von Neumann algebra to formalize non-integer, non-necessarily positive (R) degrees of freedom in General Relativity...

Hi there, have a wonderful next year!
I'm here because I have a doubt. I was trying to generalize the Einstein Field Equation for Von Neumann W* Algebra, which is related with non-integer, non always positive degrees of freedom. In particular, with the sum of positive and negative fractal dimension, with two covariant indexes expressed like this:

Does it make any sense? Is it correct? How could I fix it?
Thank you so much!

 

[robphy]

Do you have references for your notation and questions?

 

[Tommolo]

Whoops! Yes, sorry! I was being too implicit, R is the Riemann tensor and μ can vary between 1,3 (just spatial dimensions) and I assumed a Von Neumann value for time (in this case, I assumed it ±1/2, but it can be a different value, see for instance Alain Connes and his works on fractal dimensions...).

 

[martinbn]

You have Ricci tensors with negative fractional indices. You need to say what that is or give a reference.

 

[Bosko]

TL;DR Summary: I was wondering about how to apply Von Neumann algebra to formalize non-integer, non-necessarily positive (R) degrees of freedom in General Relativity...

Can you provide more details, how you planing to do it ...

Hi there, have a wonderful next year!

Thank you :-)

I'm here because I have a doubt. I was trying to generalize the Einstein Field Equation for Von Neumann W* Algebra, which is related with non-integer, non always positive degrees of freedom.

Einstein field equations are defined on pseudo Riemann space (smooth space of differential geometry)
The Minkowski metric is not a true mathematical metric. (an event on the light cone of another event is at zero distance from it)

On the other side you have the Hilbert space (a metric defined as the square root of the inner product of two vectors)
On top of that space is placed the Von Neuman Algebra of bounded operators.
How will you express the terms of Einstein's field equations in this kind of space?

In particular, with the sum of positive and negative fractal dimension, with two covariant indexes expressed like this:
View attachment 337925
Does it make any sense? Is it correct? How could I fix it?
Thank you so much!

I don't understand how the fractal dimensions are defined here?

 

[PeterDonis]

I was trying to generalize the Einstein Field Equation for Von Neumann W* Algebra

Do you have a reference for this or is it your own personal research? Personal research is out of bounds for discussion here.

 

[Tommolo]

Sorry for the delay. I had no idea that this may be out of bounds here, sorry if I may have bothered you, that wasn't my intention. My reference are the article by Roger Penrose about the negative dimensionality "Application of negative dimensional tensor", 1971, and of course the classic "Negative fractal dimensions and multifractals" by Benoit B. Mandelbrot, 1990. For the Von Neumann algebra about non integer degrees of freedom, between the others, "On the dimension theory of Von Neumann algebras", 2005. So I tried to mix both in a non integer Ricci tensor <0. This is effectively due my interest in Alain Connes fractional dimensionality theories, overall the article "The idea of Connes about inherent time evolutionof certain algebraic structures from TGD point of view", by Matt Pitkanen, 2021. Another interesting point to focus this is the article "Quantum Behavior Arises Because Our Universe is a Fractal", by Young Tao, 2017. It was just a gedankenexperiment, if there are problems with that I'll remove my question, no problems whatsoever.

Now, how would I proceed to describe fractal degrees of freedoms? Well, there are many approaches, one is following the Minkowski-Boulingand,

and the second option is using the Haussdorf dimension. This led me to think about the De Sitter invariant special relativity, and its symmeties. In this way of defining dimensionality, a curve can grow like the power of 1, of 2 (a square), of 3 (cube) and so on.

But what happens with the power of -1? Well, that leads to a dynamical behaviour for even and odd values, not a homogeneous curve or a line. So, every time you reach an integer number you have a sort of rythm. (1)

A curious behaviour indeed, and I just thought it could be expressed like this, and I wonder if it made some sense.

A negative dimension in the Minkowski-Boulingand, in the Haussdorf or even the Packing dimension model, the number of the "contiguous" D-dimensional balls of dimension ε should decrease for a diminishing value of ε. In other words, there is a diminishing quantity as you "squeeze in", or...move on. This lead me to think to the number of possible outcomes of a state tending towards zero, as with adiabatic systems and entropy. (2)

Plus, inductively, one can argue that dimensions are boundaries of suitable open sets. So, for instance, an infinite serie of 0 dimensional contiguous points you get a line, a infinite series of contiguous 1D lines you get a 2D surface and an infinite number of contiguous sheets you get a volume. But for every D you have two degrees of freedom, back and forth. So to have a line you shoud draw your zero dimensional point in one side and the other, or you will get a half-line. That could be calculated easily with Minkowski-Boulingand as having a fractal dimensionality of 1/2: as you "squeeze in" ε, you get a bigger number of "balls" only in one side, not both. (3)

This means that this "special" dimensionality it has a cardinality.

So, with this, with rhytm (1), a flowing number of possible states running towards zero (2) and cardinality (3), I just wanted to explore how would behave the EFE with this kind of definition of a very strange kinds of dimensionality and it sounded me a little bit like some sort of a weird bimetric gravity, and I wanted to reach out some help to see if anyone else could help me with that. Can anyone help me fix it, please?

I also tried that with Schroedinger and that was fun too, but that's for another post ahaha!

Sorry if I bothered you again, I could remove my post as soon as you don't consider it appropriate!
Best regards and thank you again for listening me...
Thomas

 

[robphy]

To me, this is beyond the usual scope of General Relativity in this forum. Beyond the Standard Models would be more appropriate.

 

[PeterDonis]

My reference are the article by Roger Penrose about the negative dimensionality "Application of negative dimensional tensor", 1971, and of course the classic "Negative fractal dimensions and multifractals" by Benoit B. Mandelbrot, 1990. For the Von Neumann algebra about non integer degrees of freedom, between the others, "On the dimension theory of Von Neumann algebras", 2005. So I tried to mix both in a non integer Ricci tensor <0. This is effectively due my interest in Alain Connes fractional dimensionality theories, overall the article "The idea of Connes about inherent time evolutionof certain algebraic structures from TGD point of view", by Matt Pitkanen, 2021. Another interesting point to focus this is the article "Quantum Behavior Arises Because Our Universe is a Fractal", by Young Tao, 2017.

Based on this, @robphy is correct, this thread belongs in the BTSM forum. So I have moved it there.

 

[mitchell porter]

For the Von Neumann algebra about non integer degrees of freedom, between the others, "On the dimension theory of Von Neumann algebras", 2005.

I don't see anything about non-integer dimensions in that paper (I've added a link to it).

 

[Tommolo]

That is to be found on Mandelbrot's paper, which I add hereby.

Negative fractal dimension by Benoit Mandelbrot

Thanks for moving to a more coherent section of the forum (if there's any ahah) I don't want to bother, I know that somewhere I got it wrong, I'm here just to ask you exactly where and how could I fix it. Thanks and again, sorry for bothering you! :)

 

[Tommolo]

Another fundamental piece of the puzzle is the notion of a "spectra", a negative dimension, and how to interpret it. It can be really interesting to dig into this notion thanks to this wonderful book by H.R. Margolis, "Spectra and the Steenrod algebra"

Margolis "Spectra and the Steenrod algebra"

(I'm new here, so I just recently undestood how to add links, sorry...)

 

[mitchell porter]

By searching Math Overflow for posts about fractional tensors, I found posts about fractional and even complex powers of one-dimensional vector spaces. But (as Terry Tao says, quoted at first link), there are representation-theoretic barriers to generalizing arbitrary geometric concepts in this way. It may or may not be possible to generalize Riemannian geometry in the way that you intend.

edit: Since you are looking at the quantum side of things too (operator algebras), I should mention that there are plenty of formulas in particle physics that contain a dependence on the dimension d, and which can be formally generalized to non-integer d. For example, it may be possible to write expressions which supposedly describe scattering of gravitons in a space of non-integer dimension. Again, the question will be, at what point does the generalization stop making sense? Which aspects of the 4-dimensional theory can carry across, and which aspects cannot?

 

[Tommolo]

Yes, my thought experiments comes across just noting about how Green and Schwarz tried in 1984 to solve the hexagon scattering problem for string theory just adding integer degress of freedom so to achieve a reduction of the infinities coming out. In particularly, the theory seemed flawed for any even number of dimension. But non integers are never even or odd, so this made me think a little bit about it...

There is a number of hints coming out in recent years (starting from the Wheeler-deWitt equation without secundary time-like constraints and the "foliations" of space interpreted as time) that lead some to think that what we call "time" is just nothing so special at the end. Loop quantum gravity just avoid it, for instance. It just comes out eventually. But I always loved more the De Sitter approach to relativity, more geometrical and symmetrical. In a number of equation, be it the Shannon information approach to entropy

Now, for some (i.e., Rovelli or Penrose) time arrow may arise just because of the direction given by the entropy, and therefore the <0 sign could be euristically significant.

On the other side, Minkowski metric interval is given by:

Where time is again represented with minus sign. So I euristically tried to explore the option of it being not just a useful tool, but something more profound, and I tried to explore the eventuality.

Please note that (so to speak) my approach to relativity is the River Model by Painlevé-Gullstrand-Lemaitre, just to specify more deeply that I could be not strictly relatable to Riemann "curved" orthodox approach...

 

[Tommolo]

I read this interesting article by Alain Connes, a french mathematics and phyisicist who is doing some research about fractal dimensionality.

Classification of Injective Factors Cases II1, II∞, IIIλ, λ ≠ 1

He classified in this 1976 paper the Von Neumann algebras M in various subcathegories. In the case we are considering here, it could be a type IIIλ (for 0 < λ ≤ 1) of Von Neumann algebra, or a special version of it with reversed cardinality, running from infinity towards zero instead of being from zero towards infinity. The lenght of this infinitely large axis T is halving again and again, bringing far end (the zeroth coordinate) closer to the origin of the axis, yet being infinitely away.
It seems indeed a negatively oriented Hilbert space, or a Hilbert matrix maybe (ok, this seems unlikely...)

This could be in some case interpreted by time-flowing like behaviour, maybe.

Or that is what I try to conjecture.

Halving the lenght of the T axis towards the origin, the lenght of the complex vector reduces with a ratio of the square root for every halving. Now, since the solution for √(−1) =±i, there should be a double sense of flowing, creating a double arrow of time, I conjecture, that's why I try to describe it like ±(1/2) the covariant index of µ.

Or of course this could be completely wrong, which is very likely the case...

 

[Tommolo]

...something like that, I guess...

 

[Tommolo]

A way to interpret how "Minkowski" metric can be seen is through the simmetries of a de Sitter invariant special relativity theory (see file attached). The infinitesimal angle of the rotations in de Sitter invariant special relativity (dS-ISR) maybe could be seen as a negative fractal degree of freedom, a tic-toc of what can be seen as "time". It translation "removes" informations, making it becoming unaccessable from the observers. Time could hipothetically seen as something removing "options" of next moves of the observers from his/her space phases, making collapse the psi wavefunction at every tic-toc (Planck time) and at everywhere (Planck unit of space). At every tic-toc the future chances halves and the information entropy grows. Can this maybe be seen as a Minkowsk-Bouligand behaviour for a negative and fractal dimension?

 

[Tommolo]

Here the Shannon-Von Neumann entropy graphics for time as half negative dimensions. If you consider it being described by a Hilbert matrix, maybe (and just maybe) you could explain from this the Born rule: -1/2 is the power of each probability of the wavefunction to be in a given state.

So, if spacetime is constantly "moving" at a rythm given by a Planck distance lenght every Planck time (which appears to be both the maximum and the minimum spacetime "movement" admitted at high energies-speed and very small scales), this could be considered in the dS-ISR as a universal minimum (infinitesimal) angle of rotation for the fourth dimension, aka: time.

Putting it in plain words: time is halving the chances you have of doing whatever you want for each Planck time and Planck unit, and it is increasing the impossibility (or unaccessibility) of information (aka: entropy) for each tic-toc and every single point of this asyptotically de Sitter space-time.

 

[Tommolo]

So, the equation should be something like this (maybe):

R_(-𝜏)μν+R_𝜏μν=0
where μ,ν can have a value between 1 and 3 and are non negative and integers, that is, with 6 degrees of freedom (up, down; back and forth; left and right), while 𝜏 has a value of 1/2 (that is, just one degree of freedom: time can just go forward OR backwards, according to the arrow of time) and can be negative and non-integer.

The equation therefore has sort of 10 terms like the EFE (1/2 or -1/2 depending to the arrow of time of each "universe" and 9 terms derivating from μν)

 

[berkeman]

Thread is closed for Moderation...

 

[PeterDonis]

After moderator review, the thread will remain closed.