- #1
fluidistic
Gold Member
- 3,950
- 264
Hi,
I've been thinking a while on the problem but I don't know how to proceed and if the method I'm thinking of is the most efficient.
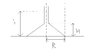
A reversed funnel (see the figure I posted) is on a table. We fill the funnel with water until the water reaches the height h. Because when it does so, the water starts to flow from the bottom of the funnel. (that is, it raises the funnel a little bit in order to flow).
Find the mass of the funnel.
2. The attempt at a solution
I realize I must find what net force the water create on the walls of the funnel when the water is filled up to an height of h.
But it seems very complicated since the shape of the funnel is relatively complicated and I think I must integrate the force exerted starting from the table level up to the height H.
If you could help me to start the problem I'd be happy.
I've been thinking a while on the problem but I don't know how to proceed and if the method I'm thinking of is the most efficient.
Homework Statement
A reversed funnel (see the figure I posted) is on a table. We fill the funnel with water until the water reaches the height h. Because when it does so, the water starts to flow from the bottom of the funnel. (that is, it raises the funnel a little bit in order to flow).
Find the mass of the funnel.
2. The attempt at a solution
I realize I must find what net force the water create on the walls of the funnel when the water is filled up to an height of h.
But it seems very complicated since the shape of the funnel is relatively complicated and I think I must integrate the force exerted starting from the table level up to the height H.
If you could help me to start the problem I'd be happy.