A rope, a pole, and some tension

[Quantum Psi Inverted]

A rope wraps an angle θ around a pole. You grab one end and pull with a tension T0. The other end is attached to a large object, say, a boat. If the coefficient of static friction between the rope and the pole is µ, what is the largest force the rope can exert on the boat, if the rope is not to slip around the pole?

I'm struggling to understand the diagram depicted here:

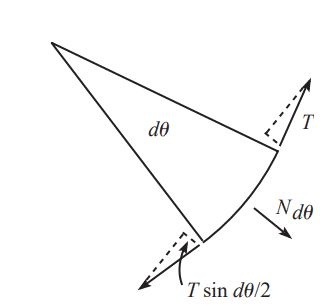
Could someone explain why this diagram would help us? This is the David Morin Classical Mechanics book if that helps whatsoever.

 

[Baluncore]

Welcome to PF.

Is this homework?

Consider a rope that passes one turn around a fixed cylinder. Then consider two turns.

The force that pulls the rope onto the friction cylinder surface, is determined by the tension you apply to the "free" end of the rope, that you are holding.

How does the tension vary along the rope?

 

[Quantum Psi Inverted]

Ah! When you put it that way, everything makes sense now. Thank you very much.

 

[Juanda]

This might be related to your interest.
https://en.wikipedia.org/wiki/Capstan_equation

 

[Delta2]

How does the tension vary along the rope?

If the rope is taken to be massless the tension is the same everywhere!

 

[haruspex]

If the rope is taken to be massless the tension is the same everywhere!

No, no! Please withdraw that.

 

[Delta2]

ok tell me where is the mistake, we take a portion dx of the rope at position x, if the rope is massless from newtons 2nd T(x+dx)-T(x)=dma=rdxa, r=0 so unless we have infinite acceleration T(x+dx)-T(x)=0 hence T constant everywhere.

 

[haruspex]

ok tell me where is the mistake, we take a portion dx of the rope at position x, if the rope is massless from newtons 2nd T(x+dx)-T(x)=dma=rdxa, r=0 so unless we have infinite acceleration T(x+dx)-T(x)=0 hence T constant everywhere.

There is a normal force from the pole, as shown, and friction parallel to the rope.
Follow the link in post #4.

 

[Delta2]

Hm. Ok so it is the same along each segment of the rope, but between the two segments it is different?

 

[Delta2]

Capstans btw is for different situation, rope multiple tied around a pole with dimensions, here the rope just does a single tie around a dimensionless pole.

 

[jbriggs444]

Capstans btw is for different situation, rope multiple tied around a pole with dimensions, here the rope just does a single tie around a dimensionless pole.

The pole is not point-like. It has a finite size. Although the diameter of the pole is unknown, that diameter will turn out to be irrelevant. The diagram is a strong hint that this is the intent.

The text indicates that there are two forces. One unknown force from the boat and one known force from you (the person holding the other end of the rope).

I've cinched up more than a few ropes wrapped around trees. And tied off mooring ropes to a fair number of cleats. I assure you that the scheme is viable.

 

[Baluncore]

Capstans btw is for different situation, rope multiple tied around a pole with dimensions, here the rope just does a single tie around a dimensionless pole.

The fixed cylinder, or bollard, is used to hold a large tension force, by multiplying the small tension force that can be applied by a person. The person cannot pull the object providing the large force nearer, but by reducing the hand tension, can hold or control it as it moves away.

A capstan is a rotating cylinder. The capstan obeys the same physics and mathematics as the bollard. The difference with the capstan is that the person can provide a high force to move a heavy object, by pulling gently with a hand on the end of the rope. The work is then being done by the capstan motor.