A simple question about the flow of the electricity

[DorelXD]

Hey guys! I'm trying to get a bettter undesrstanding of how the electric circuits work. But I do have a rather simple question. So, in the internal circuit we give energy to the charge. Let's say that I have an electricity source and two resitors, like this:

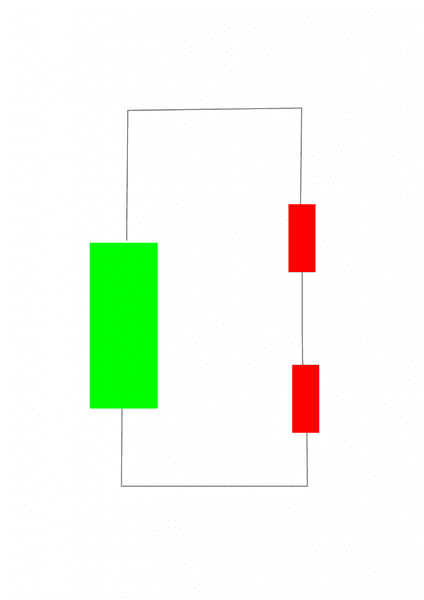
So when passing through circuit elements the charge gives up energy, so that the sum of the amount of energy it gives to each resistor is equal to the initial energy. But why? Why dosen't the charge give all the energy to the first resistor it encounters ?

And why is there no potential difference between the two red resistors? I don't get that :( . I know it's a simple concept but I can't understand why the charge loses energy only when it passes through resistors ?

 

[HallsofIvy]

Because it doesn't have to. Think of "resistance" as friction as the current passes through the resistor. There will be a certain amount of friction for the length of the resistor which causes the charge to lose energy (force times distance). The amount of energy lost depends upon the friction and distance but is not, in general, all of the energy of the current.

 

[DorelXD]

Because it doesn't have to. Think of "resistance" as friction as the current passes through the resistor. There will be a certain amount of friction for the length of the resistor which causes the charge to lose energy (force times distance). The amount of energy lost depends upon the friction and distance but is not, in general, all of the energy of the current.

Ok, I think I get it. But, from what I read, and using the model you gave me, when the charge comes out of the second red resistor it should lose al its energy, right ? So if the charge loses all the energy, then how can it go back to the source ?

 

[SteamKing]

Ok, I think I get it. But, from what I read, and using the model you gave me, when the charge comes out of the second red resistor it should lose al its energy, right ? So if the charge loses all the energy, then how can it go back to the source ?

Why should the charge lose all of its energy after leaving the second resistor? The amount of energy lost is still proportional to the amount of resistance.

 

[nsaspook]

Ok, I think I get it. But, from what I read, and using the model you gave me, when the charge comes out of the second red resistor it should lose al its energy, right ? So if the charge loses all the energy, then how can it go back to the source ?

Which resistor is the first resistor? Is it possible the energy in the circuit flows from green to red down both sides of the circuit at the same time?

 

[DorelXD]

So the movement of the electrons has nothing to do with the energy they store ?

 

[nsaspook]

So the movement of the electrons has nothing to do with the energy they store ?

Nothing is not the right word to describe the relationship in general but in a simple circuit like yours you might want to think about the electrical source and what it provides to produce current flow.

 

[CWatters]

Ok, I think I get it. But, from what I read, and using the model you gave me, when the charge comes out of the second red resistor it should lose al its energy, right ? So if the charge loses all the energy, then how can it go back to the source ?

The wire is assumed to have zero resistance.

If that's not correct and it has some resistance then the distribution of energy around the circuit will be different.

Perhaps it helps to understand that resistors are just little rods of some material that isn't an ideal conductor. So two resistors in series are equivalent to one longer rod or any number of shorter rods.

So your question..

Why dosen't the charge give all the energy to the first resistor it encounters ?

is like asking..

Why doesn't the charge give all the energy to the first few mm or μm of one of the resistors.

 

[DorelXD]

I rephrase my question. I drew a wire, and I also chose to represent two cross-section through it.

In other, word, how do I know that in the same interval of time the same amount of charge passes through the AA' and BB' ? It is quite intuitive, but I would like a justification. I can't find a simple argument, and it's driving me nuts. I can't gasp some simple concepts about electricity.

 

[NascentOxygen]

In other, word, how do I know that in the same interval of time the same amount of charge passes through the AA' and BB' ? It is quite intuitive, but I would like a justification. I can't find a simple argument, and it's driving me nuts. I can't gasp some simple concepts about electricity.

If it were to happen that in a single continuous circuit fewer charges were passing one point than another, then the only explanations could be that charge was vanishing somehow, or it was accumulating or bunching up at some point intermediate. There is no mechanism shown here that could allow either scenario.

http://imageshack.us/scaled/landing/109/holly1756.gif

 

[rude man]

I rephrase my question. I drew a wire, and I also chose to represent two cross-section through it.

In other, word, how do I know that in the same interval of time the same amount of charge passes through the AA' and BB' ? It is quite intuitive, but I would like a justification. I can't find a simple argument, and it's driving me nuts. I can't gasp some simple concepts about electricity.

Charge cannot bunch up anywhere in a circuit. Not even in a capacitor. This fact is based on one of Maxwell's equations, which says that the total voltage drops around any circuit is zero. If current bunching took place then that statement would no longer be true. Kirchhoff recognized this and formulated his KCL and KVL laws.

 

[DorelXD]

But what if the current bunched in some place ? Why isn't that possible ?

 

[NascentOxygen]

But what if the current bunched in some place ? Why isn't that possible ?

Like charges repel each other. They try to push each other apart, and the closer they are the stronger they push apart so it follows they actively work against bunching up.

There is a difference between current and charge, but I'm sure you realize this.
http://imageshack.us/scaled/landing/109/holly1756.gif

 

[DorelXD]

Like charges repel each other. They try to push each other apart, and the closer they are the stronger they push apart so it follows they actively work against bunching up.

Ohhhh, right. :) :) :) :) :) :) :)

There is a difference between current and charge, but I'm sure you realize this.

Well, current is charge that flows.

Now, please, help me to understand the KVL law. I tried to make an analogy with the gravitational field.

I would like to post my questions gradually. Here's my first.

Let the point A be at the groudn level. So, here I go: I move the object from A to B and it gains potential energy. Since the gravitational force is conservative the path dosen't matter. By moving the object back to A again it loses al the potential energy.

Now in a circuit with only a battery: I move the charge from - to + and it gains electrical potential energy. So, if I move it back to - it should get there with no potential energy, right ? So, for me it seems that the potential energy the charge gets is converted to kinetic energy, so that the charge can move back to where it came from. I don't see how we could use some of the energy of the charge to do something else with it. That is, I can't see how putting a resistor in the circuit will use the energy in another way, so that we do something useful with it.

What am I doing wrong? Is it because the charge dosen't actually convert the potential energy to kinetic energy ? That is, the movement of the charge isn't based on the potential energy it gained when it exited the internal circuity, but on the collisions with other charges ? But how's that possible? The potential energy should change while the charge is moving because it changes the position relative to the battery :( :( :( :( :( . I'm confused...

 

[nsaspook]

What am I doing wrong? Is it because the charge dosen't actually convert the potential energy to kinetic energy ? That is, the movement of the charge isn't based on the potential energy it gained when it exited the internal circuity, but on the collisions with other charges ? But how's that possible? The potential energy should change while the charge is moving because it changes the position relative to the battery :( :( :( :( :( . I'm confused...

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elevol.html#c1

 

[DorelXD]

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elevol.html#c1

Thank you, but it didin't help me.

 

[NascentOxygen]

That is not a good analogy. A higher voltage battery doesn't cause a given quantity of charge to flow in the external conductor at a greater speed; it causes more charges to flow and with an unchanged speed (if you want to put it that way).

The model you are thinking of would be thermionic emission in a vacuum tube, where electrons are liberated from the cathode and fly through a vacuum to the anode terminal of the high voltage battery. The higher the voltage, the faster the electrons are accelerated and the more KE each gains. This energy can be liberated in spectacular fashion when the electron crashes into the metal anode.

But the unimpeded flight of a charged particle through the emptiness of a vacuum is totally different to the "bucket brigade" transfer of electricity that goes on in the sea of free electrons in a metallic conductor. The electron that enters the piece of wire at one end of the battery is not the same electron that disappears back into the other end of the battery.

 

[rude man]

But what if the current bunched in some place ? Why isn't that possible ?

Well, you'd have to ask Mr. Maxwell, except he's dead.
Plus, it would violate conservation of energy.

 

[rude man]

Ohhhh, right. :) :) :) :) :) :) :)



Well, current is charge that flows.

Now, please, help me to understand the KVL law. I tried to make an analogy with the gravitational field.

I would like to post my questions gradually. Here's my first.

Let the point A be at the groudn level. So, here I go: I move the object from A to B and it gains potential energy. Since the gravitational force is conservative the path dosen't matter. By moving the object back to A again it loses al the potential energy.

Now in a circuit with only a battery: I move the charge from - to + and it gains electrical potential energy. So, if I move it back to - it should get there with no potential energy, right ? So, for me it seems that the potential energy the charge gets is converted to kinetic energy, so that the charge can move back to where it came from. I don't see how we could use some of the energy of the charge to do something else with it. That is, I can't see how putting a resistor in the circuit will use the energy in another way, so that we do something useful with it.

What am I doing wrong? Is it because the charge dosen't actually convert the potential energy to kinetic energy ? That is, the movement of the charge isn't based on the potential energy it gained when it exited the internal circuity, but on the collisions with other charges ? But how's that possible? The potential energy should change while the charge is moving because it changes the position relative to the battery :( :( :( :( :( . I'm confused...

When a mass moves from the top to the bottom the potential energy at the top changes to kinetic energy at the bottom: mgh → 1/2 mv^2.

In the case of charge q the potential energy 'at the top' changes to heat energy 'at the bottom': qE → Q
Q is the heat added
E is the battery emf.

 

[DorelXD]

Wow, I begin to understand :) . How exactly is the conservation of energy principle violated, could you please explain in more detail ? I'm dumb and I don't understand.

 

[rude man]

Wow, I begin to understand :) . How exactly is the conservation of energy principle violated, could you please explain in more detail ? I'm dumb and I don't understand.

As I said, if charge bunched up at a node then the total voltage drops around a circuit would not be zero, but that would violate the conservation of energy since the electrostatic field is conservative.

 

[haruspex]

As I said, if charge bunched up at a node then the total voltage drops around a circuit would not be zero, but that would violate the conservation of energy since the electrostatic field is conservative.

It wouldn't violate conservation of energy. In fact, bunching can occur, but the positive and negative bunches cancel out, as in a capacitor. Total charge in the circuit (including the power source) is obviously conserved, as it is a closed system. Total charge within the power source tends to be conserved because of the way the power is generated.
Even without a capacitor as such, circuits have a small amount of capacitance, and inductance. If a resistance suddenly increases some charge bunching will occur, but since the capacitance is usually low even a small bunching will generate a large voltage, tending to spread the charge out again.

DorelXD, from the OP, it seems to me that your initial misconception was that the energy was a property of the charge, and the charge somehow carried the energy around with it, spending it along the way. Rather, it is charge x voltage. The resistors being the same, there'll be the same voltage drop across each.
The wires will also have some voltage drop, since they will have a little resistance, but it's much smaller.

 

[rude man]

It wouldn't violate conservation of energy.

The OP's circuit consists of a battery and two resistors. There can be no bunching at any node therein.

Introducing parasitics in a first EE or physics course leads only to confusion by the OP.

 

[DorelXD]

DorelXD, from the OP, it seems to me that your initial misconception was that the energy was a property of the charge, and the charge somehow carried the energy around with it, spending it along the way. Rather, it is charge x voltage. The resistors being the same, there'll be the same voltage drop across each.
The wires will also have some voltage drop, since they will have a little resistance, but it's much smaller.

Thank you all for your time! It begins to make sense, but I'm still struggling a little.

 

[DorelXD]

So let's put it that way: let's say I travel to the top of the building. Say that I'm a lazy person , and for reaching the top I take the elevator. But when I go back, I take the stairs. When I first reached the top my potential energy raised. When I climbed down the stairs my potential energy went back to 0. Is that what's happening inside a circuit ? I still can't picture it clearly in my mind..

 

[haruspex]

So let's put it that way: let's say I travel to the top of the building. Say that I'm a lazy person , and for reaching the top I take the elevator. But when I go back, I take the stairs. When I first reached the top my potential energy raised. When I climbed down the stairs my potential energy went back to 0. Is that what's happening inside a circuit ? I still can't picture it clearly in my mind..

Yes, that's a reasonable model for potential. In fact, if you think of height x gravitational acceleration as being the potential and your mass as charge then multiplying the two gives the potential energy.

 

[DorelXD]

So, I'm trying to explain this to myself.

Ok, this is clear. So: I'm traveling up by elevator: I'm gaining gravitational potential energy. I'm climbing down the stairs: my potential energy is lost. But, let's suppose that by climbing down the stairs I don't get where I left from ; that is I don't arrive exactly at the doors of the elevator. To come back to where I left from, I must use some kinetic energy, correct ?

Well, let's look at the charge. It travels through the battery and it gains potential energy, right? Then, when it exits the battery it starts its journey through the connecting wires. Question:

From the end of the battery to the beginning of the restior, what type of energy does the charge use ? Does it convert it's potential energy to kinetic energy ?

Or is this an incorrect thinking? I'm thiking that the charge packs the energy and transports it to the resistor. Or in fact, the energy is transmited by collisions, I don't know how to put it, like a wave? I know that the electrons move very slowly, and for that reason, my judgement seems a bit odd.

Could someone clarify this, please?

 

[haruspex]

So, I'm trying to explain this to myself.

Ok, this is clear. So: I'm traveling up by elevator: I'm gaining gravitational potential energy. I'm climbing down the stairs: my potential energy is lost. But, let's suppose that by climbing down the stairs I don't get where I left from ; that is I don't arrive exactly at the doors of the elevator. To come back to where I left from, I must use some kinetic energy, correct ?

Well, let's look at the charge. It travels through the battery and it gains potential energy, right? Then, when it exits the battery it starts its journey through the connecting wires. Question:

From the end of the battery to the beginning of the restior, what type of energy does the charge use ? Does it convert it's potential energy to kinetic energy ?

Or is this an incorrect thinking? I'm thiking that the charge packs the energy and transports it to the resistor. Or in fact, the energy is transmited by collisions, I don't know how to put it, like a wave? I know that the electrons move very slowly, and for that reason, my judgement seems a bit odd.

Could someone clarify this, please?

The analogue of KE would be a magnetic field generated by inductance, maybe, but there is none here.
Your mistake is in thinking of the connecting wires as having no resistance. They're just more resistors, but with much smaller values.

 

[ehild]

There is potential difference between the terminals of the battery. A resistor is connected to the terminals with wires, but the resistor is also a long wire. So there is a conductive path between the terminals of the battery, you can imagine it as a single wire. There is potential difference between the ends of the wire. At the negative terminal, the electrons feel a repulsive force so they move away from the terminal. At the positive terminal, the electrons of the metal are attracted. There is an electric field in the whole wire, which accelerates the electrons toward the positive terminal. The electrons gain some extra velocity parallel to the wire. You know that the electrons of the metal perform random motion. During their random motion, the electrons collide with the atoms of the metal, and loose their extra velocity gained from the electric field. As the result they will "drift" inside the wire with a constant velocity, proportional to the electric field intensity. That drift velocity is much smaller than the velocity of their random motion, and the KE associated with it can be ignored with respect to their average thermal KE. The extra energy the electrons gained from the field is added to the vibrating atoms, increasing their vibration amplitude, which means that the temperature of the metal increases. The electric energy of the battery is converted to heat inside the wires and the resistor. We say that the electric energy is dissipated when current flows through a resistor. The dissipated power is P=UI, U is the potential difference across the resitor and I is the current flowing through it.
When you climb down on stairs, your potential energy decreases, but your kinetic energy does not increase in average as you descend. Making one step, some of your PE is converted to KE, but arriving to the next step, you loose that extra velocity, by "colliding" with the stair. The change of PE converts to the elastic energy of your muscles, to chemical energy, and to heat, at the end.

ehild

 

[DorelXD]

I believe I understand now. My picture of electric flow is much clearer. But still, how comes that the intensity of the current is constant? While passing through resitors, why doesn't the current "slow down" ? How are we sure that the flow is indeed a constant ?

Don't get me wrong! I understand that what comes in must definitely come out. But how comes that it goes out, at the same rate? Well, if two people enter a room through a door the two people will definitley come out sooner or later. Let's say that the first grabs a cup of coffee and the exits, and the second exits after he takes a nap. The electrons are very very dense, I get this. Is their tendency of repulsion that keeps them from gathering ?

 

[haruspex]

I believe I understand now. My picture of electric flow is much clearer. But still, how comes that the intensity of the current is constant? While passing through resitors, why doesn't the current "slow down" ? How are we sure that the flow is indeed a constant ?

Don't get me wrong! I understand that what comes in must definitely come out. But how comes that it goes out, at the same rate? Well, if two people enter a room through a door the two people will definitley come out sooner or later. Let's say that the first grabs a cup of coffee and the exits, and the second exits after he takes a nap. The electrons are very very dense, I get this. Is their tendency of repulsion that keeps them from gathering ?

It might help if you understand that the velocity of an electrical signal is much greater than the rate of movement of the electrons. Imagine electrons equally spaced along a wire. An extra electron is somehow added to one end. Repulsion will, at the speed of light, cause the next electron to start moving, which sets the next one moving, and so forth. Hence, though bunching may occur after some sudden event, like throwing a switch, it is so fleeting that it would be hard to measure.
For your analogy with people, you'd have to imagine them desperately trying to preserve their personal space.

 

[DorelXD]

It might help if you understand that the velocity of an electrical signal is much greater than the rate of movement of the electrons. Imagine electrons equally spaced along a wire. An extra electron is somehow added to one end. Repulsion will, at the speed of light, cause the next electron to start moving, which sets the next one moving, and so forth. Hence, though bunching may occur after some sudden event, like throwing a switch, it is so fleeting that it would be hard to measure.
For your analogy with people, you'd have to imagine them desperately trying to preserve their personal space.

That is a very good analogy, sir, thank you. So the presence of another person is very quickly noticed by the other person. He barely touches the floor with one toe and everybody is like: "go, go,go".

Good , you made this very clear and for that I'm deeply grateful. Another thing: when the electrons pass trough a resistor they must exit at the same rate, for the sam reason, is that correct ? I now completely understand that if there is no resitor the flow rate is definitely constant. But what about the flow through a resistor? Can you please tell me if the following thinking is correct?

I want to go back to the analogy I made earlier. I'm traveling up in a building, and I'm gaining potential energy. When I climb down the stairs, it takes me a while. But what if many many persons where climbing down the stairs, and my presence would be immediately noticed? That is, as soon as I put a toe on a step, the other persons notice and they immediately push each other, so that as soon as I'll be on a step with both feet, another person will have been on the floor level, right ? I now strongly believe that this is what happens.

And as off-topic I have two questions for you all:

1) do my questions show that I'm dumb? I'm worried that I don't gasp some concepts that fast. I mean...I solved electricity problems before, but I just applied formulas. I even used Kirchoff's laws without truly knowing what I was doing. Is that a problem?

2) did I annoye you? I really didn't mean that. I know I was a little bit inconsistent with my questions and I posted them in a chatoic fashion...

P.S. : I apologize again for my language, but I am not a native speaker. I am constantly learning! Thank you!

 

[nsaspook]

And as off-topic I have two questions for you all:

1: It's not dumb at all. You came to the problem with a first impression mental picture of 'mechanical electricity' energy used in many basic electronics 'viewpoint' courses in the world that's very electron/current/energy centric because it provides easy answers to common steady-state circuit parameter problems. That view is also reinforced by the common usage of 'current/amps' to represent 'power' in consumer and utility power goods. That mental picture had years of reinforcement patterns attached to it so it's not easy to just ignore or modify.

2: We have all had the same questions and most of us let you discover answers in your own way.

 

[DorelXD]

Thank you! I have one more question. As I said, I am now aware that the flow of the current must be constant. But there is still something a little bit foggy in my head. I know that when passing through a battery a charge gains energy and I understood the concept of voltage. In my old picture, this seemed very simple: a positive charge (conventional curent, I also understood that) goes from - to + and it gains potential energy.

The problem that arose in my head is the following: when we first start the circuit, an electron dosen't have time to make this journey through the internal circuit. The electrons that are close to the negative terminal "push" the electrons that are close to the positive one. But for a charge to gain an energy of, let's say 2 Volts, it must travel the whole length of the battery, right ? Then, what's happening inside a battery? Because in my head, an electron that is at the bottom, gradually picks up electric potential energy as it advance to the positive terminal. But obviously, until that electron will reach the positive terminal and will enter the external circuit, many others electrons will have left the internal circuit. How much energy have those electrons ?

 

[ehild]

Do not imagine that an electron travels along the whole path from one terminal of the battery to the other one. Outside the battery, you have a long row of electrons, pushing each other and this "push" travels very fast near the speed of light, while the electrons move forward quite slowly. Inside the battery, there are some chemical reactions which produce charge on the electrodes. The material of one electron dissolves in the electrolyte in form of positive ions, leaving electrons behind and making the electrode negative. At the other electrodes, positive ions deposit on the electrode removing electrons from it and making it positive. No need to travel through the battery... The speed of the chemical reactions determine how big current the battery can supply.
ehild