- #1
- 1,126
- 642
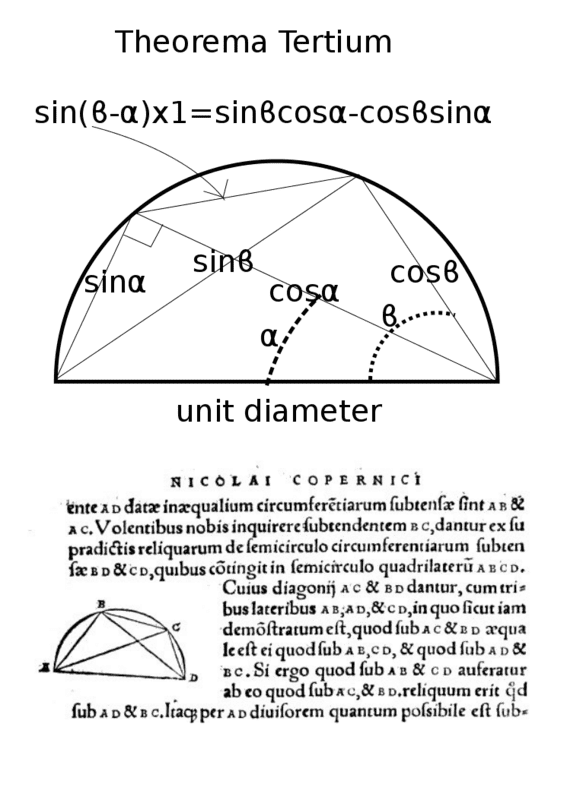
Thought following might be of interest - application of Ptolemy's Theorem from "De Revolutionibus Orbium Coelestium: Liber Primus".
Last edited by a moderator:
A Snippet of History: Application of Ptolemy's Theorem
- Thread starter neilparker62
- Start date
-
- Tags
- Application History Theorem
In summary, the conversation discusses a visual proof of a trigonometric identity and the possibility of a purely geometrical proof. The proof involves constructing a unit diameter and using the Pythagorean Theorem. A translation of a Latin text by Ptolemy is also mentioned.
- #2
- 13,368
- 3,518
Amazing visual proof of the trigonometric identity, but 2 things are not clear to me.
1. Why is the upper chord ##\sin(\beta-\alpha)##?
2. What would a purely geometrical (i.e. trigonometry-free) proof of the equality "chord times diameter equals diagonals' product minus the product of the other chords" be?
1. Why is the upper chord ##\sin(\beta-\alpha)##?
2. What would a purely geometrical (i.e. trigonometry-free) proof of the equality "chord times diameter equals diagonals' product minus the product of the other chords" be?
- #3
- 1,126
- 642
1. Construct a unit diameter from either end of the chord. Complete right triangle by joining end of diameter to other end of chord.dextercioby said:
2. Translate the Latin
(don't worry - I'll type out a translation from Stephen Hawking's book "On the Shoulders of Giants")- #4
- 1,126
- 642
In the triangle ABCD with diameter AD, let the straight lines AB and AC subtending unequal arcs be given. To us, who wish to discover the chord subtending BC, there are given by means of the aforesaid (Porism aka Pythagoras Thm) the chords BD and CD subtending the remaining arcs of the semi-circle and these chords bound the quadrilateral ABCD in the semicircle. The diagonals AC and BD have been given together with the three sides AB, AD and CD. And as has already been shown:
rect AC,BD = rect AB,CD + rect AD,BC
Therefore
rect AD,BC = rect AC,BD - rect AB,CD
Accordingly in so far as the division may be carried out:
(rect AC,BD - rect AB,CD)/AD = BC
Further when, for example, the sides of the pentagon and the hexagon are given from the above, by this computation a line is given subtending 12 degrees - and it is equal to 20791 parts of the diameter.
rect AC,BD = rect AB,CD + rect AD,BC
Therefore
rect AD,BC = rect AC,BD - rect AB,CD
Accordingly in so far as the division may be carried out:
(rect AC,BD - rect AB,CD)/AD = BC
Further when, for example, the sides of the pentagon and the hexagon are given from the above, by this computation a line is given subtending 12 degrees - and it is equal to 20791 parts of the diameter.
FAQ: A Snippet of History: Application of Ptolemy's Theorem
What is Ptolemy's Theorem?
Ptolemy's Theorem is a mathematical concept developed by the ancient Greek astronomer and mathematician, Claudius Ptolemy. It states that in a cyclic quadrilateral (a four-sided figure inscribed within a circle), the product of the diagonals is equal to the sum of the products of the opposite sides.
When was Ptolemy's Theorem discovered?
Ptolemy's Theorem was first introduced in Ptolemy's book, "Almagest," which was published around 150 AD.
What is the significance of Ptolemy's Theorem?
Ptolemy's Theorem has been used in various fields, including astronomy, geometry, and engineering. It has also been applied in solving complex trigonometric equations and determining the position of celestial bodies.
How is Ptolemy's Theorem applied in history?
Ptolemy's Theorem was used by ancient civilizations, such as the Greeks and Egyptians, to accurately predict the movements of the planets and stars. It also played a crucial role in the development of trigonometry and navigation.
Can Ptolemy's Theorem still be used today?
Yes, Ptolemy's Theorem is still used in modern mathematics and engineering. It is also a fundamental concept taught in geometry and trigonometry courses.
Similar threads
Insights
An Introduction to Theorema Primum
Studying
Balancing Theory and Applications?