Theexploer
- 7
- 2
- Homework Statement
- - Calculate the intensities of the forces applied to the sphere. Choose the cOy coordinate system shown in the diagram.
- Calculate the radius of the sphere.
friction is non-existent.
- Relevant Equations
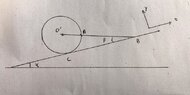
- A sphere of mass m = 150g of radius r = O'C = O'A is held in equilibrium on a perfectly smooth inclined plane by a wire AB of length l = 0.25m.
The angle between the inclined plane and the horizontal is a = 10*.
The angle between the inclined plane and the wire AB is Beta = 20*.
The sum of the forces should be 0.
Sin A'C'B' = px/b
px = mg . sin alpha
P should be px = - m.g. sin alpha and py = m.g.cos alpha
Finally i fund as result F = -0.8 and R = -1.23
but for the second question i didn't fund the radius of the circle.
Sin A'C'B' = px/b
px = mg . sin alpha
P should be px = - m.g. sin alpha and py = m.g.cos alpha
Finally i fund as result F = -0.8 and R = -1.23
but for the second question i didn't fund the radius of the circle.