lorenz0
- 151
- 28
- Homework Statement
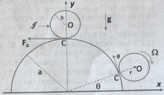
- A sphere of radius ##b##, mass ##m##, moment of inertia ##I_0## sits on the top of a hemisphere of radius ##a## with friction coefficient ##\mu##. An impulse ##J## is applied horizontally to the center of the sphere.
The friction ##\vec{F}_a## is such that the sphere can roll without slipping.
The sphere moves along the hemisphere until reaching angle ##\theta_D## (known), and at that point it loses contact with the hemisphere.
Find:
a) The relationship between the angular velocity of the sphere with respect to its center of mass ##\Omega## and the angular velocity of the center of mass of the sphere with respect to the center of the hemisphere ##\dot{\theta}##;
b) The angular velocity ##\Omega## and the kinetic energy just after the impulse is applied;
c) The angular velocity of the center of mass at ##\theta_D##;
d) Magnitude of the friction force for angles ##\theta>\theta_D##
e) The horizontal component of the velocity of the point of the sphere that touches the ground, at ##y=0##.
- Relevant Equations
- ##\vec{J}=\Delta\vec{p}##, ##v=\Omega r##, ##E=K+U##, ##\vec{\tau}=\vec{r}\times\vec{F}=I\alpha##
a) From impulse-momentum theorem I have: ##J=mv## so ##v=\frac{J}{m}## and since the ball doesn't slip ##v=\Omega b## so ##\Omega=\frac{J}{mb}## and ##\dot{\theta}=\frac{v}{a+b}=\frac{\Omega b}{a+b}##.
b) I considered the angular impulse: ##-J(a+b)=I_0 \Omega_0 \Rightarrow \Omega_0=-\frac{J}{I_0}(a+b)##.
For the energy I have: ##\fbox{E}=mg(a+b)\sin(\theta)+\frac{1}{2}mv^2+\frac{1}{2}I_0 \Omega^2## and since the sphere is rolling without slipping ##v=\Omega b## hence ##E=mg(a+b)\sin(\theta)+\frac{1}{2}m(\Omega b)^2+\frac{1}{2}I_0 \Omega^2=mg(a+b)\sin(\theta)+\frac{1}{2}(I_0+mb^2)\Omega^2##.
c) Using conservation of energy I have: ##E_i=mg(a+b)+\frac{1}{2}(I_0+mb^2)\Omega_0^2, E_f=\frac{1}{2}\Omega_D^2 (I_0+mb^2)+mg(a+b)\sin(\theta_D)## so from ##E_i=E_f## I get ## \Omega_D=\sqrt{\Omega_0^2+\frac{2mg(a+b)(1-\sin(\theta_D))}{I_0+mb^2}} ##.
d) ##-bF_a=I_0 \alpha \Rightarrow |F_a|=|-\frac{I_0}{b}\frac{d\Omega}{dt}|##, where ##\Omega=\sqrt{\Omega_0^2+\frac{2mg(a+b)(1-\sin(\theta))}{I_0+mb^2}}\overset{(b)}{=}\sqrt{(-\frac{J}{I_0}(a+b))^2+\frac{2mg(a+b)(1-\sin(\theta))}{I_0+mb^2}}##.
e) ##v_x= - b\Omega_D## (negative since the rotation is clockwise)
-----
I am quite unsure about how I solved this problem so I would appreciate if someone would check it out and give me some feedback. Thanks.
b) I considered the angular impulse: ##-J(a+b)=I_0 \Omega_0 \Rightarrow \Omega_0=-\frac{J}{I_0}(a+b)##.
For the energy I have: ##\fbox{E}=mg(a+b)\sin(\theta)+\frac{1}{2}mv^2+\frac{1}{2}I_0 \Omega^2## and since the sphere is rolling without slipping ##v=\Omega b## hence ##E=mg(a+b)\sin(\theta)+\frac{1}{2}m(\Omega b)^2+\frac{1}{2}I_0 \Omega^2=mg(a+b)\sin(\theta)+\frac{1}{2}(I_0+mb^2)\Omega^2##.
c) Using conservation of energy I have: ##E_i=mg(a+b)+\frac{1}{2}(I_0+mb^2)\Omega_0^2, E_f=\frac{1}{2}\Omega_D^2 (I_0+mb^2)+mg(a+b)\sin(\theta_D)## so from ##E_i=E_f## I get ## \Omega_D=\sqrt{\Omega_0^2+\frac{2mg(a+b)(1-\sin(\theta_D))}{I_0+mb^2}} ##.
d) ##-bF_a=I_0 \alpha \Rightarrow |F_a|=|-\frac{I_0}{b}\frac{d\Omega}{dt}|##, where ##\Omega=\sqrt{\Omega_0^2+\frac{2mg(a+b)(1-\sin(\theta))}{I_0+mb^2}}\overset{(b)}{=}\sqrt{(-\frac{J}{I_0}(a+b))^2+\frac{2mg(a+b)(1-\sin(\theta))}{I_0+mb^2}}##.
e) ##v_x= - b\Omega_D## (negative since the rotation is clockwise)
-----
I am quite unsure about how I solved this problem so I would appreciate if someone would check it out and give me some feedback. Thanks.
Attachments
Last edited: