physicisttobe
- 56
- 13
- Homework Statement
- boltzmann distribution
- Relevant Equations
- …
Hi guys,
Can you give me some feedback on whether my calculation is correct? I applied the formula below (Boltzmann Distribution) but I didn‘t know what to use for the variable z. I don‘t even know if I used the correct equation. Can you help me further?
The task is:
Consider a system of independent particles that can only occupy 2 different energy levels ε0 = 0 (non-degenerate) or ε1 = 50 meV (3-fold degenerate). At what temperature do 20% of the particles have energy ε1?
Hint: k= 1.38E-23 J/K
e= 1.60E-19 As
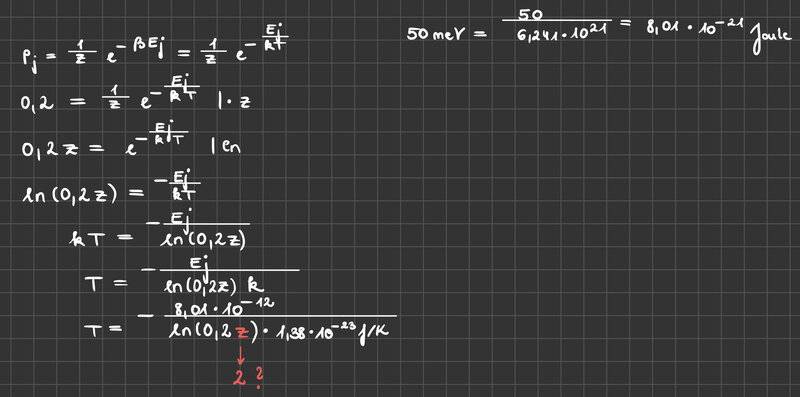
Can you give me some feedback on whether my calculation is correct? I applied the formula below (Boltzmann Distribution) but I didn‘t know what to use for the variable z. I don‘t even know if I used the correct equation. Can you help me further?
The task is:
Consider a system of independent particles that can only occupy 2 different energy levels ε0 = 0 (non-degenerate) or ε1 = 50 meV (3-fold degenerate). At what temperature do 20% of the particles have energy ε1?
Hint: k= 1.38E-23 J/K
e= 1.60E-19 As