A system of two bodies and wall

[rudransh verma]

Homework Statement

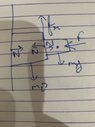
Consider the figure. The wall is smooth but the surfaces of A and B in contact are rough. Then-
1. System may remain in equilibrium
2. Both bodies must move together
3. System cannot remain in equilibrium
4. None

Relevant Equations

Newton second law.

I think there is normal force from wall and applied force will balance each other but there is no counter force against mg.Both bodies will slip and fall. I am not sure.

 

[BvU]

Did you manage to draw free body diagrams ?

[edit]

If you have to tick 1,2,3,4 (or more than one?), which is/are your best shot ?​

​

I have difficulties with this exercise: F is not mentioned in the text, but only appears in the picture ?​

​

The text uses 'remain' where you write 'be'. Also: 'must move together' and 'move together '​

Are there two versions ?​

$\$

 

[rudransh verma]

The text uses 'remain' where you write 'be'. Also: 'must move together' and 'move together 'Are there two versions ?

No I wrote it in my words and yes there is F.

 

[BvU]

Then maybe it's only my personal interpretation problem: the wording 'remain in equilibrium' can (but apparently does not have to) mean that the picture is of an equilibrium (starting) situation. Never mind.

Did you manage to draw free body diagrams ?

$\$

 

[jbriggs444]

No I wrote it in my words and yes there is F.

Would I be correct to assume that $\vec{F}$ is, as drawn, purely horizontal?
Would I be correct to assume that gravity is present and non-zero, even though it is not drawn?
Would I be correct to assume that "equilibrium" means that the system remains at rest if it began at rest?

If so, can you go through 1), 2) and 3) and explain why each holds or does not?

 

[rudransh verma]

If so, can you go through 1), 2) and 3) and explain why each holds or does not?

Force on B is balanced from all directions but not on A. There is no upward friction since the wall is smooth. So the system assuming is at rest in beginning cannot remain in rest and is not in equilibrium if that what we mean by equilibrium (rest).

 

[Steve4Physics]

Force on B is balanced from all directions

Q1. How do you know? What are the forces on B? What balances B's weight?
(Pity you haven't done free body diagrams as suggested by @BvU.)

but not on A.

Q2. How do you know? What are the forces on A?

There is no upward friction since the wall is smooth. So the system assuming is at rest in beginning cannot remain in rest and is not in equilibrium if that what we mean by equilibrium (rest).

Q3 If A and B start at rest, do you think B (which you think is in equilibrium) remain at rest?

Q4. Is there any friction between A and B? If not, why not?

Q5 (Bonus question.) If an object is in 'equilibrium' does that mean it must be at rest?

P.S. Dd you ever find the very easy way to solve your recent problem about the falling knife using potential energy and work (2 or 3 lines of simple working)? https://www.physicsforums.com/threads/knife-dropped-on-cardboard.1011687/

 

[rudransh verma]

Q1. How do you know? What are the forces on B? What balances B's weight?

Surface A and B are rough. Friction.

How do you know? What are the forces on A?

Wall is smooth.

Q3 If A and B start at rest, do you think B (which you think is in equilibrium) remain at rest?

After A slips B will too eventually.

If an object is in 'equilibrium' does that mean it must be at rest?

I think there is no acceleration.

P.S. Dd you ever find the very easy way to solve your recent problem about the falling knife using potential energy and work (2 or 3 lines of simple working)?

No!

 

[jbriggs444]

After A slips B will too eventually.

Why not immediately? What is holding it in place?

 

[rudransh verma]

Why not immediately? What is holding it in place?

Body A

 

[jbriggs444]

Body A

How is body A supposed to support body B if body A is, itself, falling down?

What forces do you imagine exist between the two of them. And why?

 

[rudransh verma]

How is body A supposed to support body B if body A is, itself, falling down?

What forces do you imagine exist between the two of them. And why?

I meant momentarily.
Friction. Given rough surface.

 

[Steve4Physics]

See Post#7 for the original quetions.

[Q1] Surface A and B are rough. Friction.

Q1. If A moves down and IF there is friction,between A and B there would be two downwards forces on B (weight and friction from A). So B would not be in equilibrium.

[Q2] Wall is smooth.

Q2. But IF A exert a frictional force on B, then B exerts an equal magnitude and opposite direction frictional force on A (Newton’s 3rd law). So B would exert a frictional force on A (even though there is no frictional force on A due to the smooth wall).

[Q3] After A slips B will too eventually.

Q3. Why ‘eventually’? What will make B start to move?

Q4. Unanswered.

[Q5] I think there is no acceleration.

Q5 You haven’t answered the question asked.
“If an object is in 'equilibrium' does that mean it must be at rest?”.
The answer is ‘yes’ or ‘no’ plus a reason.

I'll tell you the answer since it isn't directly needed to answer your Post#1 question. The answer is:
No. It would also be in equlibrium if it were moving with a constant velocity.

[P.S.] No!

P.S. How much gravitational potential energy did the knife lose in total? How much work did the resistive force do? If you can answer those two questions you can find the resistive force extremely easily.

I think you must take a step back. Drawing free body diagrams helps you to correctly think about what forces act. Until you can (correctly) draw the free body diagrams for A and B, I don't think you will be able to answer the question (IMHO).

Edited

 

[jbriggs444]

I meant momentarily.
Friction. Given rough surface.

Static friction?
Kinetic friction?

Can you reason out why neither can produce any force? Not even momentarily.

 

[hutchphd]

2

.

 

[haruspex]

I meant momentarily.
Friction. Given rough surface.

Frictional forces act to oppose the relative motion that occurs, or would otherwise occur, between surfaces in contact.
For nonzero kinetic friction between two surfaces there must be some relative motion of the bodies.
For nonzero static friction between two surfaces there must be some tendency to relative motion of the bodies. I.e. in the absence of that friction there would be relative motion between them.

 

[Steve4Physics]

@rudransh verma:

If A and B were both perfectly smooth (zero friction between them) what would happen and why?

If A and B were both stuck together (effectively infinite friction) what would happen and why?

 

[rudransh verma]

If A and B were both perfectly smooth (zero friction between them) what would happen and why?

Both will fall down because of imbalance of forces.
I have made the diagram and I think all are balanced in the OP. So equilibrium!

 

[Steve4Physics]

Both will fall down because of imbalance of forces.

Yes, they both fall. Do they fall at the same rate?

I have made the diagram and I think all are balanced in the OP. So equilibrium!

Your diagram is wrong. And the blocks are not in equilibrium.

Part of the problem is that the OP is badly worded.

Think of holding a stone stationary (in equilibrium) in your hand. You then release the stone. What force(s) act on the stone the moment after you release it? Is the stone now in equilibrium?

Think of the OP diagram as showing two blocks the moment after they were released.

 

[rudransh verma]

Think of holding a stone stationary (in equilibrium) in your hand. You then release the stone. What force(s) act on the stone the moment after you release it? Is the stone now in equilibrium?

Think of the OP diagram as showing two blocks the moment after they were released.

Gavity is acting on the stone.
If after they were released means removal of force F then both will fall.

 

[Steve4Physics]

Gavity is acting on the stone.
If after they were released means removal of force F then both will fall.

Will the (frictionless) blocks fall at the same rate? What is this rate?

Force F (in the OP diagram) acts horizontally and is always present. It does not get removed.

The force(s) initially suporting the blocks are not shown in the OP diagram. The OP diagram shows the blocks from the moment after the supporting force(s) have been removed.

 

[rudransh verma]

Will the (frictionless) blocks fall at the same rate? What is this rate?

No! Different rate since difference in mass. Acceleration due to gravity!

Force F (in the OP diagram) acts horizontally and is always present. It does not get removed.

yeah!

The force(s) initially suporting the blocks are not shown in the OP diagram. The OP diagram shows the blocks from the moment after the supporting force(s) have been removed.

What supporting forces? are you talking about normal forces and friction?

 

[jbriggs444]

What supporting forces?

There are none. We expect that the blocks begin at rest relative to each other because we are not told otherwise. We might imagine that this was arranged by having the blocks held in place until just before we start looking at the system.

 

[Steve4Physics]

No! Different rate since difference in mass. Acceleration due to gravity!

yeah

No, not different rates! Identical rates!

A heavy mass accelerates the same as a light mass (ignoring air resistance). Both have acceleration = g (= 9.8 m/s² (approx.) downwards).

What supporting forces? are you talking about normal forces and friction?

Suppose blocks A and B are initially stationary and each hang on a string.

The only supporting forces (the forces preventing the blocks falling vertically downwards) are the tensions in the strings.

Now cut both strings simultaneously!

You now have the setup described in the OP. There are now no supporting forces.

 

[rudransh verma]

No, not different rates! Identical rates!

A heavy mass accelerates the same as a light mass (ignoring air resistance). Both have acceleration = g (= 9.8 m/s² (approx.) downwards).

O right!

If A moves down and IF there is friction,between A and B there would be two downwards forces on B (weight and friction from A). So B would not be in equilibrium.

Due to weight of B there is upward friction on A but due to weight of A there is downward friction on B. So both will come down the moment they are released at same rate g.
I have two possibilities. Which one? 1 or 2 ?
What if we treat it as a system? I think both will come down because there is no upward forces on either of them.

 

[BvU]

Well, well. After 24 posts we now have free body diagrams. The reason I asked for them is that I would like you to discover that there are no vertical forces except the two from gravity. And they cause the two blocks to fall with exactly the same acceleration. That means there is no tendency for the blocks to move wrt each other in any direction.

You have drawn friction forces, but exactly because there are no other vertical forces, the actual friction forces are zero, which makes your 1) and 2) diagrams identical. At best you have drawn the maximum friction forces, something like $\mu F_N$.

 

[rudransh verma]

Well, well. After 24 posts we now have free body diagrams. The reason I asked for them is that I would like you to discover that there are no vertical forces except the two from gravity. And they cause the two blocks to fall with exactly the same acceleration. That means there is no tendency for the blocks to move wrt each other in any direction.

I think there should be no friction too because there is no upward force on any of the bodies.

 

[jbriggs444]

I think there should be no friction too because there is no upward force on any of the bodies.

But there is a downward force on both bodies. What makes upward forces special in your mind?

 

[rudransh verma]

But there is a downward force on both bodies. What makes upward forces special in your mind?

There have to be relative motion between A and B for the friction to occur here. Wall is smooth and no upward force on B. So both will fall at same rate due to gravity after we remove supporting forces.

 

[haruspex]

There have to be relative motion between A and B for the friction to occur here.

As I wrote, that is for kinetuc friction. For static friction there does not need to be any actual relative motion, only that there would be relative motion if the friction were not there.