George Plousos
- 11
- 2
I will study your notes, Ibix. In the meantime I have prepared this thought experiment:
I think I can show that the answer to the original question may be different. To achieve this I will use two additional people, Helen and Tom, but in the end I will remove these two people as if they never existed, so only Bob, Alice and Alex will remain on stage, as the original question wants. The image helps a lot.
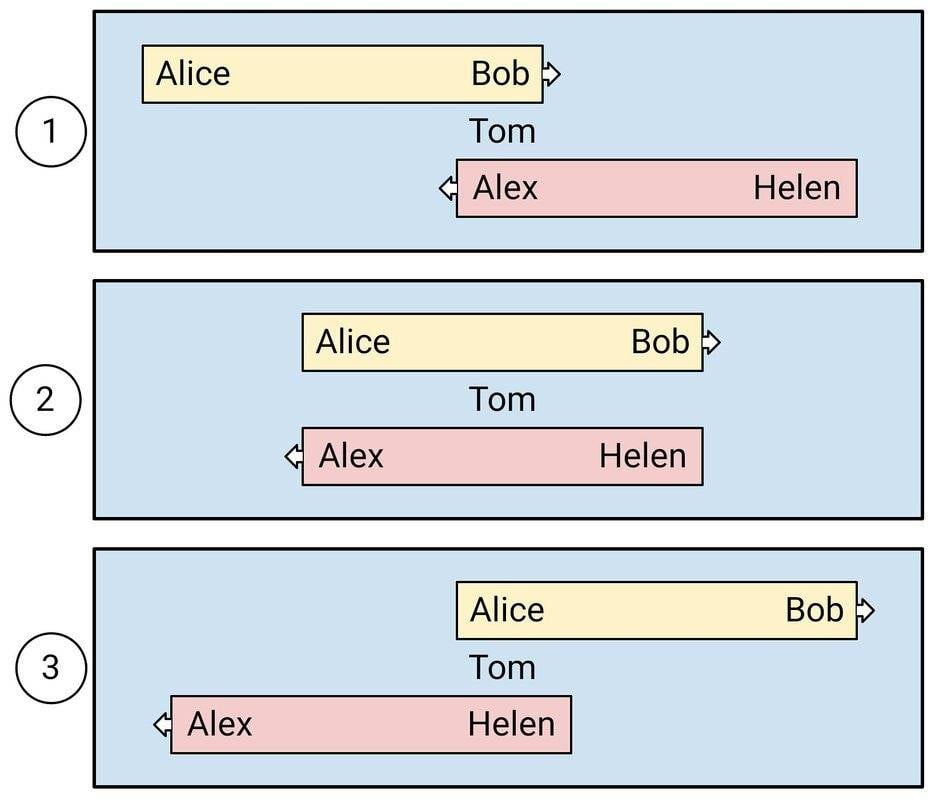
Fig 1: The distance that separates Bob from Alice in the yellow reference frame is the same as the distance that separates Alex from Helen in the pink reference frame. The clocks of the observers in each separate reference frame are synchronized with the Einstein method. Tom is considered immobile, while Bob and Alex move at the same speed in Tom's view. At the meeting point of the three boys, their three clocks are synchronized.
Fig 2: At some point along the way, Alex will meet Alice and they will be photographed with each other. At some point the same thing will happen between Bob and Helen. We will return to figure 2 later.
Fig 3: Tom meets Alice and Helen. Because of the symmetry, Alice and Helen's clocks remain synchronized in Tom's view. If you want, the two girls are photographed with each other. Immediately after this observation, Tom sees Alice and Eleni slowing down at the same speed and stopping. Obviously, in the short time between Tom's last observation and the immobilization of the girls, there is no dramatic change in their clocks, but this is true anyway because of the symmetry of the system with respect to Tom.
Now all observers are motionless with each other - they are in the same frame of reference. Alice is in sync with Bob and Helen, who is in sync with Alex. So Bob, Alice, Alex and Helen are all in sync with each other. But then all four observers must have been in sync at all stages of the journey between Figures 1 and 3. Consequently, in the events described above for Fig 2 these four observers would also be in sync. We can now forget the involvement of Helen and Tom in the experiment, to find that the same conclusions apply to the original question - we now refer to the facts of figure 2 without Helen and Tom.
The answer to the original question was that the photos between Alex and Alice would show that Alex's watch was going backwards relative to Alice's watch before Alex stopped, but based on the new arguments the same photos must show that their clocks have remained in sync.
I can not see any error in the above arguments, unless I am blind because of my prejudice, or I have not learned everything I should.
I think I can show that the answer to the original question may be different. To achieve this I will use two additional people, Helen and Tom, but in the end I will remove these two people as if they never existed, so only Bob, Alice and Alex will remain on stage, as the original question wants. The image helps a lot.
Fig 1: The distance that separates Bob from Alice in the yellow reference frame is the same as the distance that separates Alex from Helen in the pink reference frame. The clocks of the observers in each separate reference frame are synchronized with the Einstein method. Tom is considered immobile, while Bob and Alex move at the same speed in Tom's view. At the meeting point of the three boys, their three clocks are synchronized.
Fig 2: At some point along the way, Alex will meet Alice and they will be photographed with each other. At some point the same thing will happen between Bob and Helen. We will return to figure 2 later.
Fig 3: Tom meets Alice and Helen. Because of the symmetry, Alice and Helen's clocks remain synchronized in Tom's view. If you want, the two girls are photographed with each other. Immediately after this observation, Tom sees Alice and Eleni slowing down at the same speed and stopping. Obviously, in the short time between Tom's last observation and the immobilization of the girls, there is no dramatic change in their clocks, but this is true anyway because of the symmetry of the system with respect to Tom.
Now all observers are motionless with each other - they are in the same frame of reference. Alice is in sync with Bob and Helen, who is in sync with Alex. So Bob, Alice, Alex and Helen are all in sync with each other. But then all four observers must have been in sync at all stages of the journey between Figures 1 and 3. Consequently, in the events described above for Fig 2 these four observers would also be in sync. We can now forget the involvement of Helen and Tom in the experiment, to find that the same conclusions apply to the original question - we now refer to the facts of figure 2 without Helen and Tom.
The answer to the original question was that the photos between Alex and Alice would show that Alex's watch was going backwards relative to Alice's watch before Alex stopped, but based on the new arguments the same photos must show that their clocks have remained in sync.
I can not see any error in the above arguments, unless I am blind because of my prejudice, or I have not learned everything I should.