Albert1
- 1,221
- 0
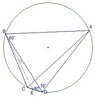
$Quadrilateral \,\,ABCD,\overline{AB}=\overline{AC} ,\angle ABD=60^o,\angle ADB=70^o,
\angle BDC=40^o,find \,\, \angle DBC=?$
\angle BDC=40^o,find \,\, \angle DBC=?$
Last edited: