- #1
kenok1216
- 58
- 1
Poster has been reminded to use the HH Template and show their work
where are the charge =0? please help...no idea how to do
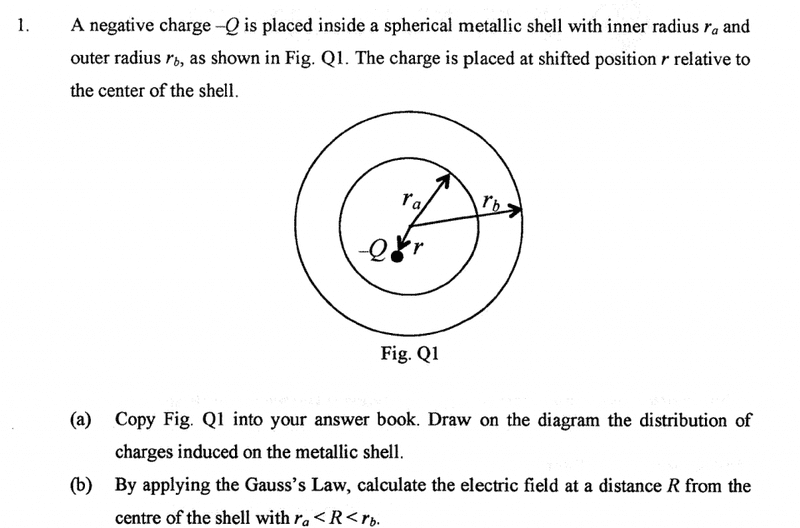
Last edited by a moderator:
