About writing a unitary matrix in another way

In summary, the conversation discusses the properties of an unitary matrix and how it can be represented in a given form. The conversation then explores how to show that a matrix satisfies a certain condition by taking the most general matrix and imposing the condition on it. The conversation also mentions using the standard formula to find the inverse of a matrix and using the hermitian to determine the relationships between the matrix's elements.
  • #1
aalma
46
1
It is easy to see that a matrix of the given form is actually an unitary matrix i,e, satisfying AA^*=I with determinant 1. But, how to see that an unitary matrix can be represented in the given way?
20230322_224305.jpg
 
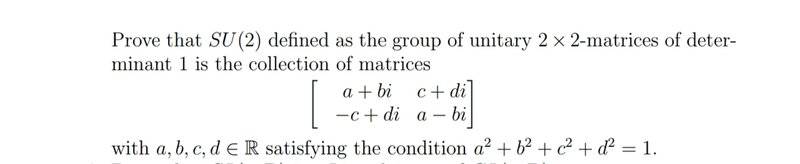
Last edited by a moderator:
Physics news on Phys.org
  • #2
Take the most general matrix,
$$
A =
\begin{bmatrix}
a + bi & c + di \\
e+ fi & g+hi
\end{bmatrix}
$$
and show that imposing ##AA^\dagger = I## requires ##e = -c##, ##f=d##, and so on.
 
  • Like
Likes aalma and topsquark
  • #3
Yes, thanks. Tried to do this however got somehow long equations with these eight real numbers. guessing how it should be solved!
I also wrote the condition that the det of this matrix=1.
 
  • #4
Can't you just find the inverse of the matrix using the standard formula, and then you do the hermitian of the matrix and thus figure out what the relationsships of a, b, c, ... must be?

##A^\dagger = A^{-1}##
 
Last edited:
  • Like
Likes aalma and DrClaude

What is a unitary matrix?

A unitary matrix is a square matrix with complex entries that satisfies the condition of being equal to its own complex conjugate transpose.

Why would someone want to write a unitary matrix in another way?

Writing a unitary matrix in another way can help simplify calculations and make certain properties of the matrix more apparent.

What is the most common way to write a unitary matrix?

The most common way to write a unitary matrix is in the form of a product of a matrix and its complex conjugate transpose, where the matrix is represented by a capital letter and its conjugate transpose by a dagger symbol.

Can a unitary matrix be written in multiple ways?

Yes, a unitary matrix can be written in multiple ways as long as it satisfies the condition of being equal to its own complex conjugate transpose.

What are some other ways to write a unitary matrix?

Other ways to write a unitary matrix include using the polar decomposition or the singular value decomposition methods.

Similar threads

I Why Use Gram-Schmidt to Make a Unitary Matrix?
    • Linear and Abstract Algebra
Replies
14
Views
1K
A Similarity transformation changing the determinant to 1
    • Linear and Abstract Algebra
Replies
20
Views
999
I Can I visualize O(3) \ SO(3) in some way?
    • Linear and Abstract Algebra
Replies
4
Views
128
I Spectral theorem for Hermitian matrices-- special cases
    • Linear and Abstract Algebra
Replies
2
Views
611
I Proving only 1 normalized unitary vector for normal matrix
    • Linear and Abstract Algebra
Replies
3
Views
1K
How can a diagonalising matrix be unitary?
    • Advanced Physics Homework Help
Replies
15
Views
1K
I Want to understand how to express the derivative as a matrix
    • Linear and Abstract Algebra
Replies
8
Views
1K
I Solving matrix commutator equations?
    • Linear and Abstract Algebra
Replies
6
Views
525
I Does a unitary matrix have such property?
    • Linear and Abstract Algebra
Replies
4
Views
1K
I Building a Unitary Matrix from a Non-Unitary Matrix
    • Linear and Abstract Algebra
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top