Abrahams-Minkowskii Controversy: Is Phonon Momentum Defined?

[pervect]

A recent thread involves some papers on the issue of determining which of the proposed laws for the momentum of a photon in a media is correct, the Abrahams or the Minkowskii momentum.

I was thinking about the issue, and I have a rather different take on the same fundamental question, one sufficiently different that I thought it needed a different thread. Rather than consider an ideal strutureless "dielectric media", let's consider a more physical model, where we have a crystal lattice with well-defined properties including but not limited to a dielectric constant. Then the process of light propagation through this lattice can be thought of as the absorption and re-emission of photons, a process that has been described (at least here on PF) as coherent scattering.

First question: Is it basically correct to say that when the photon is absorbed, it transfers its momentum to an atom in the lattice, and this creates a quantized lattice vibration, a "phonon"?

Second question: Do phonons have a definite value of momentum? This is an area outside my field of knowledge, and might be best in a quantum forum, but it's one point in the larger question which relates mostly to relativity.

The reason I suspect phonons may not have a definite value of momentum is from reading the Wiki article, https://en.wikipedia.org/w/index.php?title=Phonon&oldid=690954197

Crystal momentum

By analogy to photons and matter waves, phonons have been treated with wave vector

as though it has a momentum [PLAIN]https://upload.wikimedia.org/math/f/5/e/f5e5b0c106e07c9ea90e7f1df9b86e2f.png, however, this is not strictly correct, because https://upload.wikimedia.org/math/f/5/e/f5e5b0c106e07c9ea90e7f1df9b86e2f.png is not actually a physical momentum; it is called the crystal momentum or pseudomomentum.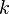

If we can meaningfully define a certain amount of momentum to the phonon, it seems to me that we can determine what part of the momentum is "photon momentum", and what part of the momentum is "crystal momentum" carried by the phonon.

If we can't, then at the moment I don't see any way of meaningfully splitting up the momentum in this manner - a point of view that has some precedent, apparently.

I do believe that the propagation speed of phonons should be slower (about the speed of sound) than the propagation of light, which suggest to me that the process of momentum transport via phonos and photons distinguishable, though at the moment I don't have a clear enough formulation to actually propose an experimental test.

There is a vast amount of literature on the Abrahams-Minkowskii issue, which I'm afraid I've barely read. So I'm hoping someone can point me in the direction of papers that might consider things from the point of view I am suggesting, or perhaps shoot it down.

 

[Dale]

I don't see any way of meaningfully splitting up the momentum in this manner - a point of view that has some precedent, apparently.

The paper that I found most convincing on the topic took this stance, but it was a purely classical paper and did not discuss photons or phonons at all.

Are you interested in classical treatments, or only quantum treatments?