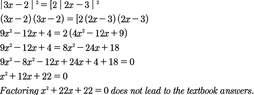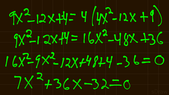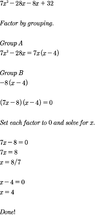mathdad
- 1,280
- 0
Solve the absolute value equation.
|3x - 2|/|2x - 3| = 2
Solution:
|3x - 2| = 2|2x - 3|
3x - 2 = 2(2x - 3)
3x - 2 = 4x - 6
Solving for x, I get x = 4.
However, the textbook has two answers for this problem.
The answer is also 8/7.
How do I find 8/7?
|3x - 2|/|2x - 3| = 2
Solution:
|3x - 2| = 2|2x - 3|
3x - 2 = 2(2x - 3)
3x - 2 = 4x - 6
Solving for x, I get x = 4.
However, the textbook has two answers for this problem.
The answer is also 8/7.
How do I find 8/7?