AC Circuit Analysis: Solving Example with Confusing Concepts

[bardia sepehrnia]

TL;DR Summary

Difficulty understanding some concepts; RMS of voltage and current with phasor.

I'm reading this chapter in Electrical Engineering book regarding AC circuit analysis where there is a solved example which I've attached, but there are some concepts that are confusing me.
First, why and how do we know that the phasor value of voltage is: -pi/2
Note: I do understand that 14.14/√2 ≈ 10 but I don't get where -π/2 comes from?

Second, earlier in the book and before the solved example the following formulas are stated:

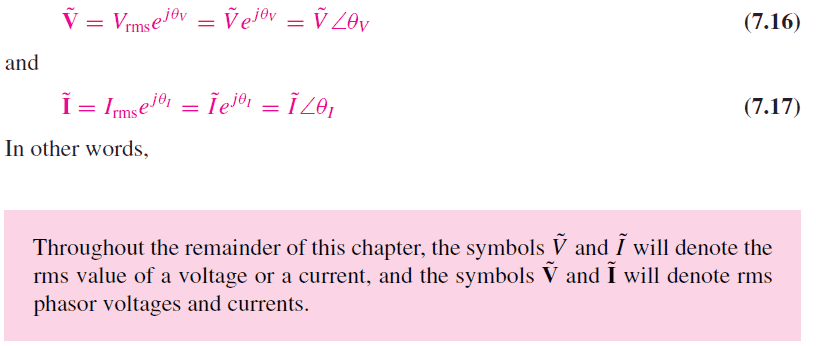
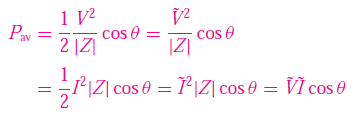
So why in calculation of average power, the italic V and I are not used. Is that a mistake on the book? Shouldn't average power only be real number and not complex? Also in the solved example only real values of I and V is used, yet the V and I are not italic.

 

[anorlunda]

$\angle\frac{\pi}{2}$ is a phase shift of 90 degrees. That is equivalent to multiplying by j as in $(R+j\omega L)$

 

[BvU]

Hi,

First, why and how do we know that the phasor value of voltage is: -pi/2

That's easy: $\ \sin(\omega t) = \cos (\omega t - {\pi\over 2})$

1. So why in calculation of average power, the italic V and I are not used. Is that a mistake on the book?
2. Shouldn't average power only be real number and not complex?
3. Also in the solved example only real values of I and V is used, yet the V and I are not italic.

I agree it's confusing. They make a mess of it in example solution 7.1..

1. Yes. in example solution 7.1 it is clear that $\tilde{\bf\text{V}}=10$ and $\tilde{\bf\text{I}}=2$ and 7.16 & 17 wants $\tilde V$ and $\tilde I$
2. Yes. And it is; do you see it otherwise ?
3. Isn't this the same question as 1. ?

You pasted a $P_{\text{av}}= ...$ picture after the 'Throughout...' where they are more consistent .

 

[bardia sepehrnia]

Thank you very much! It sounds very simple after you explained it but I just started on this topic and I'm a mechanical engineering student. Our uni started teaching us AC circuit analysis before any prior knowledge on electricity. I had to self study everything just to understand what the teacher says. First lesson he started solving equations with impedance and that was the first time I heard that term!