AC Circuit Phasors: Find I1, I2, I3

[Martin Harris]

Homework Statement

AC Circuit Phasors

Relevant Equations

Kirchoff's and Ohm's Law

Summary:: Hi, I tried attempting this problem in alternating current in order to find out the phasors as complex numbers, and I would be more than grateful if someone could peer review it, and confirm my calculations (Please see below both the Figure and the calculations)

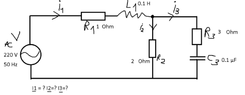
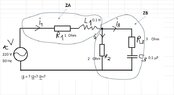
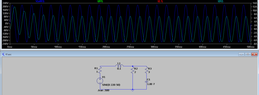
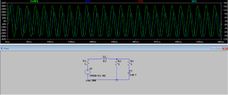
Please find attached the electrical circuit as a figure.

Given data:

Voltage V	220 V
Frequency	50 Hz
Resistance R1	1 Ω
Coil electrical inductance L1	0.1 H
Resistance R2	2 Ω
Resistance R3	3 Ω
Capacitor electrical capacitance C3	0.1 μF = 10-7 F

I1, I2, I3 =? (Phasors as complex numbers for alternating current)
From Ohm's Law:
$$I = \frac V Z (Eq1)$$where I = current, V= Voltage and Z = impedance
From Kirchoff's Law:
$$I=I1=I2+I3 (Eq2)$$
Given that branches containing R2 and R3 with C3 are in | | (parallel), then:
$$V2=V3$$
and
$$\frac{1}{Z}= \frac{1}{Z_1}+\frac{1}{Z_2} (Eq3)$$
$$Z_1=R1+iωL = R1 + i*2π*F*L (Ω)$$ where i is the imaginary part of the impedance
$$Z_1=1Ω + (2*π* 50Hz *0.1H* i) Ω $$
$$ Z1 = (1+31.41592 i)Ω $$
$$Z2=R2=2Ω$$
(Z2 just 2Ω since it's just the resistance, it won't appear as a complex number impedance)
$$Z3 = R3-ixC3 = 3 Ω-\frac{1}{2*π*F*C} = 3 Ω-\frac{1}{2*π*50Hz*10^-7 F}i Ω $$
$$Z3 = (3 - 31830.988i) Ω$$
From Eq3:
$$\frac{1}{Z}= \frac{1}{(1+31.41592 i)Ω}+\frac{1}{2Ω} $$
According to Microsoft MathSovler
$$Z=(1.987950624+0.126177045i) Ω $$

$$From Eq1: I1 = I = \frac V Z $$
$$I= \frac {220V} {(1.987950624+0.126177045i)Ω} $$
$$I1= (110.276245603−6.992857044i)A $$
$$ From Eq2 (Kirchoff's Law): I2=I1-I3 = (110.276245603−6.992857044i)A - I3 (Eq4) $$
$$ V2=V3$$ hence $$I2*Z2=I3*Z3 (Eq5)$$
Substituting Eq4 into Eq5 yields:
$$(110.276245603−6.992857044i)A * 2Ω = I3 * (3 - 31830.988i) Ω$$
Solving for I3 (According to Microsoft Math Solver)
$$I3 = (0.000440024+0.006928817i) A $$
Now from Eq5 we can solve for I2 =I1-I3
$$I2=(110.276245603−6.992857044i)A - (0.000440024+0.006928817i) A$$
$$I2 = (110.27576−6.999728 i)A$$

I am really confused why I3 is so low though, for sure I did something wrong because I3 has negative value both on the real and imaginary part.

I would be more than grateful if someone could check my work as a peer review.

 

[Gordianus]

The imaginary part of Z3 has the wrong sign. I didn't check the magnitude.

 

[Martin Harris]

The imaginary part of Z3 has the wrong sign. I didn't check the magnitude.

Hi
Thanks for your reply, I looked again at it
I assumed $$Z3 = R3 (resistance real part) + iXC3 (imaginary part of the impedance)$$
so $$Z3 = 3 Ω + i*(\frac {1} {2*π*50Hz*10^-7F })Ω$$
$$Z3=(3Ω+i*(\frac {1} {π*0.00001})Ω)$$, right?

 

[Gordianus]

The modulus of the capacitive reactance Is OK. However, the imaginary unit should carry a negative sign.

 

[Martin Harris]

The modulus of the capacitive reactance Is OK. However, the imaginary unit should carry a negative sign.

Right I understood, thanks for that, well spoted! Perhaps I carried on the sign from the coil over to the capacitor, so the coil should be +ve and the capacitor -ve.

By having $$Z3=R3-iXC3$$

And $$ I = I1 =I2+I3 $$

I get:
$$I= I1 = (110.276245603−6.992857044i)A $$
$$I3 = (0.000440024+0.006928817i) A $$
$$I2 = (110.27576−6.999728i) A$$

Now I am confused because I3 seems tiny...whilst I1 and I2 seem huge compared to I3...

I got no idea if these values are even correct, not sure if the work I did is correct though

 

[Gordianus]

No wonder I3 Is small. The modulus of Z3 Is quite large compared with Z1 and Z2.

 

[Martin Harris]

No wonder I3 Is small. The modulus of Z3 Is quite large compared with Z1 and Z2.

Yes, you're right.
What can you tell about the values on I1 and I2? Do they make any sense? I'm not sure if values for I1 and I2 are right though...

 

[Gordianus]

I'm using my phone and checking complex math with a small screen isn't simple.
I suggest checking the results with KCL and KVL.

 

[Martin Harris]

Yes, well I used KCL to get I2=I1-I3, having calculated I=I1=V/Z and I3 from I2Z2=I3Z3
My general Z was calculated as 1/Z = 1/Z1+1/Z2

 

[Gordianus]

I've been following this thread with my phone and I can hardly read it. When I get back home I'll check the numbers.

 

[Gordianus]

I just checked with a big screen. Eq 3 is wrong. Look at the circuit.

 

[Babadag]

First you forgot part ZA by considering Z=ZB only.
Second in my opinion Z[=ZB]=1.99999998026079-0.000125663703042964i

 

[Martin Harris]

I just checked with a big screen. Eq 3 is wrong. Look at the circuit.

You're absolutely right, now I did:
$$ Z_overall = Z1 + \frac {Z2*Z3} {Z2+Z3}$$
Then
$$ I = I1 = \frac {V} {Z_overall} =\frac {220} {(2.99999998+31.415794336i)} $$
Final results:
$$I1=(0.662682446−6.939565186i)A$$
$$I2=(0.662246414−6.939606755i)A$$
$$I3 =(0.000436032+0.000041569i)A$$

 

[Baluncore]

I agree with the result, but there are some rounding errors.

Z1 = R1 + XL1 = ( +1.000000000000 +31.415926535898 j ) ohm;
Z2 = R2 + 0 = ( +2.000000000000 +0.000000000000 j ) ohm;
Z3 = R3 + XC1 = ( +3.000000000000 -31830.988618379070 j ) ohm;

Z23 = Z2 // Z3 = ( +1.999999980261 -0.000125663703 j ) ohm;
Z123 = Z1 + Z23 = ( +2.999999980261 +31.415800872195 j ) ohm;

Vin = Vrms = ( +220.000000000000 +0.000000000000 j ) volt;
I1 = Vin / Z123 = ( +0.662682172378 -6.939563768654 j ) amp;
V23 = I1 * Z23 = ( +1.324492280395 -13.879210675423 j ) volt;

I1 = Vin / Z123 = ( +0.662682172378 -6.939563768654 j ) amp;
I2 = V23 / Z2 = ( +0.662246140197 -6.939605337712 j ) amp;
I3 = V23 / Z3 = ( +0.000436032181 +0.000041569057 j ) amp;

 

[Gordianus]

Please, be lenient with this comment.
Where can I buy a 15 digit voltmeter?

 

[Baluncore]

Where can I buy a 15 digit voltmeter?

You don't need to. Just simulate it with double precision.
Different approaches lead to different numerical stability and rounding patterns.
You can write a ladder network as a continued fraction.
Attenuators attenuate the differences.
Amplifiers amplify the differences.

 

[Baluncore]

Please, be lenient with this comment.

Our results agreed to only six digits, I would have expected much better numerical agreement.

There must be a reason why we differ. After a bit of detective work …

For reactance evaluation I used Pi = 4 * Atn(1) = 3.141592653589793
The value of Pi used to evaluate post #13 was; 3.141592000000000
That now perfectly explains all our numerical differences.

I am numerically happy.

 

[Martin Harris]

I agree with the result, but there are some rounding errors.

Z1 = R1 + XL1 = ( +1.000000000000 +31.415926535898 j ) ohm;
Z2 = R2 + 0 = ( +2.000000000000 +0.000000000000 j ) ohm;
Z3 = R3 + XC1 = ( +3.000000000000 -31830.988618379070 j ) ohm;

Z23 = Z2 // Z3 = ( +1.999999980261 -0.000125663703 j ) ohm;
Z123 = Z1 + Z23 = ( +2.999999980261 +31.415800872195 j ) ohm;

Vin = Vrms = ( +220.000000000000 +0.000000000000 j ) volt;
I1 = Vin / Z123 = ( +0.662682172378 -6.939563768654 j ) amp;
V23 = I1 * Z23 = ( +1.324492280395 -13.879210675423 j ) volt;

I1 = Vin / Z123 = ( +0.662682172378 -6.939563768654 j ) amp;
I2 = V23 / Z2 = ( +0.662246140197 -6.939605337712 j ) amp;
I3 = V23 / Z3 = ( +0.000436032181 +0.000041569057 j ) amp;

Hi
Just a question, how do we know 220V is the rms though? I was just given 220V and thought that's the peak value

 

[Baluncore]

Hi
Just a question, how do we know 220V is the rms though? I was just given 220V and thought that's the peak value

The international mains voltage is now about 230 Vrms = 325 Vpeak.
Like you, SPICE assumes a 220 V sinewave oscillates between ±220 V = 220 Vpeak.

Since it was not specified otherwise, I assumed that the 220 V was most likely to be Vrms.
The currents I computed are therefore also RMS.

The computation of VA power and VAR differ for Vrms and Vpeak.

 

[Martin Harris]

The international mains voltage is now about 230 Vrms = 325 Vpeak.
Like you, SPICE assumes a 220 V sinewave oscillates between ±220 V = 220 Vpeak.

Since it was not specified otherwise, I assumed that the 220 V was most likely to be Vrms.
The currents I computed are therefore also RMS.

The computation of VA power and VAR differ for Vrms and Vpeak.

Hi
Thanks a lot for the quick reply! It is much appreciated.
Please find attached the SPICE simulation results for 220V and 311V
are also peak. I was just given 220V though.
Now, I'm confused, am I doing something wrong? Because I assumed 220V is peak and hence the currents

What voltage should I put into SPICE Simulation then? 220V or 311V? Since I want to correlate the simulation with the manual calculations. I'm confused now if the currents calculated by manual work are peak or rms.

 

[Baluncore]

What voltage should I put into SPICE Simulation then? 220V or 311V?

A physicist or mathematician might assume; V = 220;
An engineer or technician might assume; V = 220 Vrms * √2;

I'm confused now if the currents calculated by manual work are peak or rms.

It really does not matter which you used. They all stay the same.
If it is not specified, make a decision, state it clearly, then stick to it.

Only if you will evaluate power do you need to know if it is Vrms or Vpk.
The integration of instantaneous (v*i) over a full cycle will give you real power.

If you avoid the integration;
The product of Vrms and in-phase current, Irms.real, will give real power.
The product of Vpk and Ipk.real requires a factor of ½ to give real power.

 

[Martin Harris]

A physicist or mathematician might assume; V = 220;
An engineer or technician might assume; V = 220 Vrms * √2;It really does not matter which you used. They all stay the same.
If it is not specified, make a decision, state it clearly, then stick to it.

Only if you will evaluate power do you need to know if it is Vrms or Vpk.
The integration of instantaneous (v*i) over a full cycle will give you real power.

If you avoid the integration;
The product of Vrms and in-phase current, Irms.real, will give real power.
The product of Vpk and Ipk.real requires a factor of ½ to give real power.

Thanks a lot! I understood!
Now I'm trying to figure out why I1 roughly = I2 and I3 is so small
I think becauseso little current is shunted to the R3C3, hence I2 roughly = I1
Little current I3 because capacitor C3 = 0.1 micro Farad

I mean, what makes it that I3 is so small, hence I1=I2?
From Kirchoff's Law, I1=I2+I3
I3 is small due to Z3, hence I2 has to be roughly I1

 

[Baluncore]

I mean, what makes it that I3 is so small, hence I2=I3?
From Kirchoff's Law, I1=I2+I3
I3 is small due to Z3, hence I2 has to be roughly I1

I think you mean, I3 is small, hence I1 ≈ I2.

I3 is small because C1 is small, 0μ1 F.
At 50 Hz, XC1 is huge = -31k831 ohm.

I3 is also lower than you might expect because;
the voltage across Z3 is lowered by the presence of XL1.
XL1 = +31.41 ohm, which is big compared to the 1 ohm of real series resistance in Z1.

 

[Martin Harris]

I think you mean, I3 is small, hence I1 ≈ I2.

I3 is small because C1 is small, 0μ1 F.
At 50 Hz, XC1 is huge = -31k831 ohm.

I3 is also lower than you might expect because;
the voltage across Z3 is lowered by the presence of XL1.
XL1 = +31.41 ohm, which is big compared to the 1 ohm of real series resistance in Z1.

Thanks a lot! Yeah, sorry about that, I was thinking of Kirchoff's Law already when I was typing it, so please consider it a typo.

For V2=V3=V23 I got 14V, as I did the magnitude, seems about right I guess (?)

 

[Baluncore]

For V2=V3=V23 I got 14V, as I did the magnitude, seems about right I guess (?)

V23 = I1 * Z23 = ( +1.324492280395 -13.879210675423 j ) volt;
V23 mag = 13.9422655 V, phase = -84.548775°.

 

[Martin Harris]

V23 = I1 * Z23 = ( +1.324492280395 -13.879210675423 j ) volt;
V23 mag = 13.9422655 V, phase = -84.548775°.

Yeah, I just rounded it to 14V, but you're more precise! Thanks a lot! By the way how did you get that phase?
I got phase around -80°

 

[Baluncore]

By the way how did you get that phase?

Given complex V23 = ( +1.324492280395 -13.879210675423 j ) volt;

Function Amplit( Byval a As complex ) As Double
Return Sqr( a.real * a.real + a.imag * a.imag )
End Function

Function Phase( Byval a As complex ) As Double
Return Atan2( a.imag, a.real )
End Function
Then convert radians to deg.