AC - Node Voltage Method for difficult circuit

[devmew]

Hi!
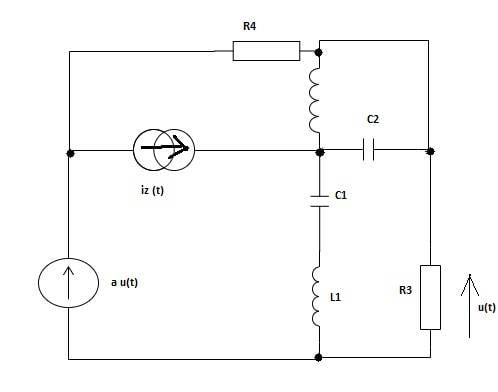
I'm trying to understand and solve this circuit by Node Voltage Method. I have to calculate u(t). In my mind, I don't have any idea if any current should go through Z1 in my calculations.
I would be grateful if you could write even equations for this circuit. Is 'a' just a prefix to multiply the value of voltage source? (z is the letter for 'complex' in my language).

Data:
iz(t)=2cos(2t−45°) A C1=1/2 [F] C2=1/3 [F] L1=1[H] L2=3[H]
R3=2[Ω] R4=1[Ω] a=1/2 [V/V]

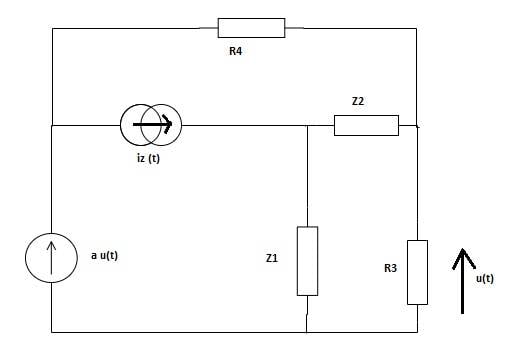
My calculations:
Iz=1+j; ω=2rad/s; Z1=j; Z2=-2j


Thank you in advance.

 

[berkeman]

Welcome to PhysicsForums.

Is a*u(t) a VCVS? That seems like a non-standard voltage source symbol, but it does look like you are using a different symbol for the iz(t) source...

Also, I don't see how the 2nd circuit follows from the first, but I could be missing something. Were you given the 1st circuit and you wanted to simplify it via the 2nd diagram?

 

[Babadag]

a=e^(-j*2*π/3)=cos(-2*π/3)+jsin(-2*π/3)

 

[Babadag]

I=√2.[cos(-45o)+j.sin(-45o)]=1-j

 

[devmew]

@berkeman a*u(t) is only hint, needed to calculations. It describes the relationship between voltage source and voltage on resistor. 'a' is just a coefficient. I was given the first circuit and I wanted to simplify it via 2nd diagram.
@Babadag I'm looking to get the value u(t) in function of sinx. So, I changed it into sin function.
$$i_z(t)=2cos(2t-45°)=2sin(2t-45°+90°)=2sin(2t+45°)$$
$$I_z=\frac{2}{\sqrt{2}}(cos(45°)+j sin(45°))=\frac{2}{\sqrt{2}}(\frac{\sqrt{2}}{2}+j\frac{\sqrt{2}}{2})=1+j$$

a*u(t) is the voltage source, and iz(t) is the power source. I'm sorry, I didn't know the worldwide symbols.

$$Z_1=\frac{1}{jωC_1}+jωL_1=\frac{1}{j}+2j=-j+2j=j$$
$$\frac{1}{Z_2}=\frac{1}{jωL_2}+jωC_2$$
$$Z_2=\frac{6}{3j}=-2j$$