rudransh verma
Gold Member
- 1,067
- 96
- Homework Statement
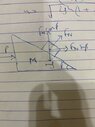
- A wedge and a block are moving on a smooth horizontal surface such that the block of mass m is at rest with respect to wedge of mass M. The magnitude of applied force P
- Relevant Equations
- ##F=ma##
I have drawn a fbd and the logic I think is that at rest the block moves down the wedge but when a force P is applied vertical force becomes zero and the horizontal force ##F_N\sin \beta## = P?
Attachments
Last edited: