Acceleration and Displacement from a Velocity vs. Time Graph

[gnits]

Homework Statement

Find the acceleration and displacement of a particle from its velocity versus time graph

Relevant Equations

a=dv/dt

Please could I ask for help with the following question:

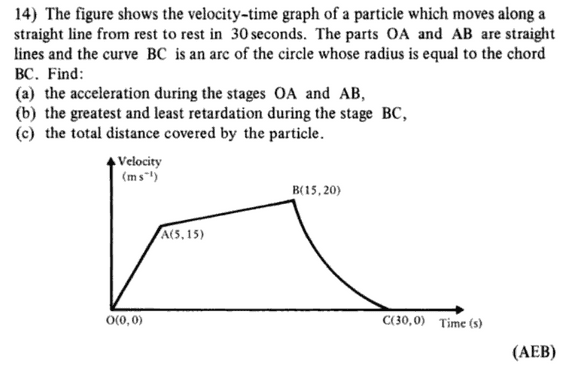
Part (a) is no problem. Acceleration is the gradient of the graph in regions OA and AB which gives 3 and 0.5

Part (b), I believe, requires me to calculate the greatest and least value of the gradient of the curve in region BC

Part (c), I believe, requires me to calculate the area under the whole graph.

My question is, can I solve parts (b) and (c) without working out the equation of the circle? Unless I have miscalculated, the equation of the circle is not particularly simple, the centre is not nicely located on integral values of x and y.

My working was that the length of the chord is sqrt(15^2+20^2) = 25 and so to get the centre of the circle in order to find it's equation I should have to solve the following system:

(x-15)^2+(y-20)^2 = 625
(x-30)^2+y^2=625

Once I had the equation of the circle I would differentiate it to find max min gradients and integrate it to find area under it.
is this the way to go?

The answers the book gives are:

(b) (1/3)*(24 + 13*sqrt(3)) and (1/3)*(24 - 13*sqrt(3))

(c) 258

Thanks,
Mitch.

 

[Delta2]

I think for (c) you definitely need the equation of the circle. I don't see any other way cause you have to integrate to find the area under the curve BC.
But for (b) I got no clue what your book means by retardation. If it means deceleration then it wants you to find the maximum and minimum of v'(t), so i think you ll have to look for solutions to the equation v''(t)=0.

 

[jbriggs444]

I think for (c) you definitely need the equation of the circle. I don't see any other way cause you have to integrate to find the area under the curve BC.

If you are looking to find the area under a curve, integration is not the only approach. Geometry works too.

 

[Delta2]

If you are looking to find the area under a curve, integration is not the only approach. Geometry works too.

Ok I can't disagree with that but I still think he needs to find the center of the circle in order to do it with the geometric approach.

 

[jbriggs444]

Ok I can't disagree with that but I still think he needs to find the center of the circle in order to do it with the geometric approach.

The area of an equilateral triangle and the area of a 60 degree sector of a circle can both be determined without bothering about the location of the center.

 

[Delta2]

The area of an equilateral triangle and the area of a 60 degree sector of a circle can both be determined without bothering about the location of the center.

Ok I think I see your approach, quite clever I should say. It involves the area of an isosceles triangle as well right?

 

[jbriggs444]

Ok I think I see your approach, quite clever I should say. It involves the area of an isosceles triangle as well right?

We are given that the chord is equal to the radius. To me, that says "equilateral". But yes, I think you have grasped the scheme.

 

[Delta2]

We are given that the chord is equal to the radius. To me, that says "equilateral". But yes, I think you have grasped the scheme.

Besides the area of the equilateral triangle and the area of respective circular sector we also need the area of the triangle BCD into the calculations, where D the point on x-axis below B, don't we?

 

[jbriggs444]

Besides the area of the equilateral triangle and the area of respective circular sector we also need the area of the triangle BCD into the calculations, where D the point on x-axis below B, don't we?

Oh, that. It is a right triangle (15, 20, 25 it looks like) not isosceles. I was just considering that as part of computing the area of a trapezoid quadrilateral -- too easy to worry about.

 

[gnits]

Thanks for all the replies. Looking at part (c) I want to calculate the area under the whole graph. Can anyone see an error in this calculation? Area of 60 degree sector = (1/2)*25^2*PI/3 = 327.25. Area of equilateral triangle = (1/2)*25^2*sin(60) = 625*sqrt(3)/4 = 270.63. So area of segment 327.25 - 270.63 = 56.62. So area under circular part of graph = Area of (15,20,25) triangle - 56.62 = (1/2)*15*20 - 56.62 = 93.38 and so area under whole graph = (1/2)*5*15+150+(1/2)*10*5+93.98 = 305.88 NOT 258 :( Thanks for any help, Mitch.

 

[Delta2]

Thanks for all the replies. Looking at part (c) I want to calculate the area under the whole graph. Can anyone see an error in this calculation? Area of 60 degree sector = (1/2)*25^2*PI/3 = 327.25. Area of equilateral triangle = (1/2)*25^2*sin(60) = 625*sqrt(3)/4 = 270.63. So area of segment 327.25 - 270.63 = 56.62. So area under circular part of graph = Area of (15,20,25) triangle - 56.62 = (1/2)*15*20 - 56.62 = 93.38 and so area under whole graph = (1/2)*5*15+150+(1/2)*10*5+93.98 = 305.88 NOT 258 :( Thanks for any help, Mitch.

I can't spot any mistake in the above calculation...

 

[gnits]

Thanks for checking. It's really uncharacteristic for the book I am working from to have wrong answers. When it does it's usually just an obvious sign missing or something similar. I did part (b). Can anyone confirm whether my working looks correct. Firstly I derived the equation of the circle as (x - (45/2 + 10*sqrt(3)) )^2 + (y - ( 10+15*sqrt(3)/2) )^2 = 625. It can be easily seen that the points (15,20) and (30,0) are on this circle so I am confident that this is the correct equation. Now I differentiate this to get dy/dx = (-x-(45/2)+10*sqrt(3)) / (y -10-15*sqrt(3)/2) and then I put in x = 15 and y = 20 to get the maximum gradient. This gives dy/dx = -8.3 so my answer would be 8.3 but book says (1/3)*(24 + 13*sqrt(3)) which is 15.5. Thanks for any verification or otherwise. Mitch.

 

[jbriggs444]

I ran the same numbers without looking at your calculations and got the same answer.

My notes:

Let us start with the area of a quadrilateral bounded below by the x-axis and above by:

Line segment from (0,0) to (5,15). This triangle is 5 units wide by 15 units high. Area = 5*15/2 = 37.5
Line segment from (5,15) to (15,20). The average height is (15+20)/2. Multiply by width 10. Area = 35*10/2 = 175
Line segment from (15,20) to (30,0). This triangle is 15 units wide by 20 units high. Area = 15*20/2 = 150

Add them up and we get 325+37.5 = 362.5

But we have to subtract out that crescent-shaped segment where the circular arc eats into the quadrilateral.

I get $\frac{1}{6}\pi r^2$ = 327.25 for the area of the circular sector and $\frac{r^2\cos 30}{2}$ = 270.63 for the area of the equilateral triangle. (r=25 of course). The delta is 56.62 for the crescent.

Subtract 56.62 from 362.5 and get 305.88

 

[neilparker62]

Thanks for checking. It's really uncharacteristic for the book I am working from to have wrong answers. When it does it's usually just an obvious sign missing or something similar. I did part (b). Can anyone confirm whether my working looks correct. Firstly I derived the equation of the circle as (x - (45/2 + 10*sqrt(3)) )^2 + (y - ( 10+15*sqrt(3)/2) )^2 = 625. It can be easily seen that the points (15,20) and (30,0) are on this circle so I am confident that this is the correct equation. Now I differentiate this to get dy/dx = (-x-(45/2)+10*sqrt(3)) / (y -10-15*sqrt(3)/2) and then I put in x = 15 and y = 20 to get the maximum gradient. This gives dy/dx = -8.3 so my answer would be 8.3 but book says (1/3)*(24 + 13*sqrt(3)) which is 15.5. Thanks for any verification or otherwise. Mitch.

Also getting 8.3 as maximum gradient by finding the centre D (22.5 + 10√3 ; 10 + 7.5√3) and hence gradients of DB and DC. Maximum gradient will be that of tangent line perpendicular to DB and minimum gradient that of tangent line perpendicular to DC.

 

[Williambecker1]

Great job you are doing. Keep it up. I really like it

 

[gnits]

Thanks averybody for all of your help. I'm going with our answers and in this case assuming that the book is incorrect. Thanks again, Mitch.