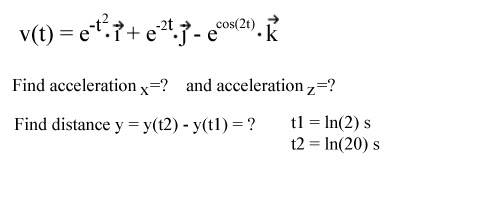Acceleration and distance using derivatives.

In summary, the conversation discusses the concept of deriving and integrating velocity to find acceleration and distance. The person asking for help is unsure if they are using the correct approach and is seeking clarification on their work. They are also struggling with integrating e^x and are advised to use the substitution method. Eventually, they are able to correctly derive and integrate the equation.
  • #1
Bman900
12
0
Now I understand the basic concept that if one derivative's velocity you get acceleration and if you integrate velocity you will get the distance. But what about in this case?

Homework Statement


problem1.jpg

Homework Equations


The Attempt at a Solution


attemptedsolution-1.jpg
 
Physics news on Phys.org
  • #2
You didn't differentiate properly. You need the chain rule(s).

So, I'm thinking you probably didn't integrate correctly, either.

But, we don't know, as you didn't post your results.
 
  • #3
Well I didn't get to that yet because I was not sure that is the correct way of finding the answers. So am I at least derivating the right parts of the equation?
 
  • #4
For what the problem is asking, yes - that's the correct approach.
 
  • #5
Ok so I derivated but I could not integrate because I have only know e^x. Am looking into to solving that but please tell me if the answers so far are correct?

attemptedsolution-2.jpg
 
  • #6
The a_x is correct, but not a_z. What is the derivative of cos?

And for the integration, set -2t to u, so that you integrate e^u. Don't forget that you are now integrating with respect to u!
 
  • #7
Oh its -sin so the negative signs cancel out! Thanks. Am am about solve the integral here soon as I have to learn a bit more about the substitution method.
 
  • #8
Am I correct?

integrate.jpg
 
  • #9
Looks good to me!
 

FAQ: Acceleration and distance using derivatives.

What is acceleration?

Acceleration is the rate of change of velocity over time. It is a vector quantity and is measured in meters per second squared (m/s^2).

What is the formula for acceleration?

The formula for acceleration is a = (v2 - v1) / t, where v2 is the final velocity, v1 is the initial velocity, and t is the time interval.

How is acceleration related to distance?

Acceleration is related to distance through the use of derivatives. The derivative of the distance function with respect to time is velocity, and the derivative of velocity with respect to time is acceleration.

How do you calculate distance using derivatives?

To calculate distance using derivatives, you must integrate the acceleration function with respect to time. This will give you the velocity function, which can then be integrated again to get the distance function.

Why are derivatives important in understanding acceleration and distance?

Derivatives are important because they allow us to analyze the behavior of acceleration and distance functions in more detail. They help us understand the relationship between acceleration, velocity, and distance, and how they change over time.

Similar threads

Relating acceleration to distance and time
Replies
5
Views
2K
Displacement given the acceleration
Replies
8
Views
1K
How to Apply Derivatives in Physics Problems?
Replies
9
Views
580
Solving for Work Done When Accelerating a Mass
Replies
3
Views
143
Deriving the particle's motion using numerical integration
Replies
5
Views
338
Derivation of an expression for centripetal acceleration
Replies
3
Views
2K
Find the acceleration in circular motion
Replies
6
Views
1K
Acceleration of a shot put ball
Replies
3
Views
2K
Deriving an equation for the velocity of a particle
Replies
1
Views
871
Block and pulley on movable incline
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top