Acceleration and thrust of a rocket

[warfreak131]

Hey guys, I want to know if I have an equation on thrust correct. I figured what's the acceleration as a function of time.

You have the upward thrust = dm/dt v, assuming the mass flow rate and the gas ejection rate is constant

and the downward force = -m(t) g, where m=m(t) since it's losing fuel as it travels

so:
dm/dt v - m(t) g = m(t) a

where m(t) = m0 - dm/dt t

dm/dt v - (m0 - dm/dt t)g = (m0-dm/dt t)a

Divide both sides by m(t)

(dm/dt v)/(m0 - dm/dt t) - g = a

I plotted this function for dm/dt = 10, v = 10, m = 1000

The red line represents the acceleration, and the blue line represents the velocity. The acceleration line looks correct, like the acceleration starts off slow, but as the rocket loses mass, it begins to accelerate at a faster rate, but the velocity is where I'm concerned, why is the initial velocity almost -700 m/s?

 

[Simon Bridge]

dm/dt v - m(t) g = m(t) a

How do you figure this?

Surely:
$$\sum F = \frac{dp}{dt} = v\frac{dm}{dt}+m\frac{dv}{dt}$$

See:
http://en.wikipedia.org/wiki/Tsiolkovsky_rocket_equation

 

[cryora]

Not sure why upward thrust is dm/dt v

Isn't F_net = dp/dt = d(mv)/dt = dm/dt v + m dv/dt ?

So gravity: F_g = - m(t) g
Trust: F_t = ?

F_net = F_g + F_t = -m(t)g + F_t = dm/dt v(t) + m(t) dv/dt

v(t) = v₀ + dv/dt t

So

-m(t)g + F_t = dm/dt (v₀ + dv/dt t) + m(t) dv/dt
-m(t)g + F_t = dm/dt v₀ + dm/dt dv/dt t + m(t) dv/dt

dv/dt = (F_t - m(t)g - dm/dt v₀ ) / [dm/dt t + m(t)]
= [F_t - (m₀ + dm/dt t)g - dm/dt v₀] / (dm/dt t + m₀ + dm/dt t)
= ( F_t - m₀g - dm/dt gt - dm/dt v₀ ) / (dm/dt t + m₀ + dm/dt t)
= (F_t - m₀g - dm/dt (gt + v₀) / (2 dm/dt t + m₀)

Then I guess you can select arbitrary constants for F_t, m₀, v₀, dm/dt. For v₀ we can probably assume it's 0.

 

[bahamagreen]

Your model will use less fuel if your throttle takes into account the dynamic load of the atmosphere - the interplay between increasing air speed and decreasing air density with elevation.

When the rocket's air speed comes to equal the exhaust gas exit speed, the fuel is being deposited without any residual forward or backward velocity into the still air behind the rocket. This is peak efficiency. The period of flight enjoying this peak may be extended with careful management of the throttle with respect to air speed and atmospheric density.

 

[arildno]

This is completely wrong, from most posters. See post 4 in the following thread, and for that matter, the rest of it.
https://www.physicsforums.com/showthread.php?t=72176

 

[willem2]

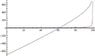
I plotted this function for dm/dt = 10, v = 10, m = 1000

The red line represents the acceleration, and the blue line represents the velocity. The acceleration line looks correct, like the acceleration starts off slow, but as the rocket loses mass, it begins to accelerate at a faster rate, but the velocity is where I'm concerned, why is the initial velocity almost -700 m/s?

Your result of a = \frac { v \frac {dm}{dt} } {m_0 - t \frac {dm}{dt} } - g is correct, note that v is the exhaust speed of the rocket, and not the speed of the rocket itself.
I've no idea how you got the graph however.

If you want to solve the differential equation, you can choose the initial position and the initial speed. Ordinarily you would choose 0 for both, and then there is no way in which the initial speed suddenly could become -700m/s, because the initial acceleration is finite.

If the exhaust speed is 10 m/s (very slow for any kind of rocket), the inital acceleration is
10*10/1000 - g = -9 m/s, so the rocket is far too weak to lift itself off the ground.
The graph for the acceleration, really can't be correct whatever your exhaust spee is, since the acceleration after 80s with only a fifth of the mass left, should be at least 5 times as big as the initial acceleration.

 

[D H]

Surely:
$$\sum F = \frac{dp}{dt} = v\frac{dm}{dt}+m\frac{dv}{dt}$$

Surely not.

This is completely wrong, from most posters. See post 4 in the following thread, and for that matter, the rest of it.
https://www.physicsforums.com/showthread.php?t=72176

That, too, is wrong.

There's no difference between F=ma and F=dp/dt for constant mass systems. There's a huge difference between the two for variable mass systems, and (IMHO) the only definition that makes sense in this case is F=ma. With F=ma, force is measurable and it is invariant across all inertial reference frames. With F=dp/dt, force is not measurable and it is a frame-dependent quantity. Yech! The vast majority of people who work with dynamic mass systems use F=ma, not F=dp/dt.
This imbroglio over F=ma vs F=dp/dt has made everyone miss the key problem in the original post. So, going back to the OP,

The red line represents the acceleration, and the blue line represents the velocity. The acceleration line looks correct, like the acceleration starts off slow, but as the rocket loses mass, it begins to accelerate at a faster rate, but the velocity is where I'm concerned, why is the initial velocity almost -700 m/s?

warfreak131, you didn't show us how you calculated velocity, so there's no knowing where you went wrong.

We have
a = \frac{dv}{dt} = \frac{\dot m}{m_0-\dot m t} v_e - g
where $\dot m$, $m_0$, $v_e$, and $g$ are constants. Note well: There are two velocities here. One is $v$, the velocity of the rocket. The other is $v_e$, the effective velocity of the exhaust with respect to the rocket.

This is a first order linear ordinary differential equation. There's no mention of the initial velocity. It's an arbitrary constant. You know the value of that arbitrary constant; it's zero in a frame in which the the rocket is at rest at t=0. The solution to that ODE is similar to that of the ideal rocket equation. The addition of the (constant) downward gravitational adds a slight twist. It's still a linear ODE, so all the tools that apply to linear ODEs still work on this problem.

 

[arildno]

"
https://www.physicsforums.com/showthread.php?t=72176

That, too, is wrong.

There's no difference between F=ma and F=dp/dt for constant mass systems. There's a huge difference between the two for variable mass systems, and (IMHO) the only definition that makes sense in this case is F=ma. With F=ma, force is measurable and it is invariant across all inertial reference frames. With F=dp/dt, force is not measurable and it is a frame-dependent quantity. Yech! The vast majority of people who work with dynamic mass systems use F=ma, not F=dp/dt."
------------------------------
Which is what that thread is working on. Don't say anything is wrong when you clearly haven't read it.

 

[warfreak131]

warfreak131, you didn't show us how you calculated velocity, so there's no knowing where you went wrong.

I calculated velocity of the rocket by integrating the function for acceleration w.r.t time.

Not sure why upward thrust is dm/dt v

Isn't that how thrust is defined?

is correct, note that v is the exhaust speed of the rocket, and not the speed of the rocket itself.

Yes, I am aware. In my original post, I specified that v was for gas ejection. Although I should have specified that the velocity in the graph is the velocity of the rocket.

 

[D H]

I calculated velocity of the rocket by integrating the function for acceleration w.r.t time.

The problem is that you haven't show us how you did that. You obviously did something wrong. We can't help you find out what you did wrong if you don't show us what you did.

So, how did you do that integration?