- #1
~christina~
Gold Member
- 714
- 0
[SOLVED] Acceleration of free falling object on another planet
A ball is shot vertically upward from the surface of another planet.
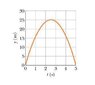
A plot of y versus t for the ball is shown in the figure below, where y is the height of the ball above its starting point and t = 0 at the instance the ball is shot.
The figure’s vertical scale is set by ys = 30.0 m.
(a) Write expressions for the displacement and velocity of the ball as functions of time.
(b) What is the magnitude of the free-fall acceleration on the planet?
(c) What is the magnitude of the initial velocity of the ball?
~I've attatched a pic of the graph.
I have to get the acceleration.
a.) I need help on how to derive a equation from that graph and I don't know what the ys= 30m scale is that they describe.
I do know that since it is x vs. t graph I can get the v from that.
b.) would I solve the equation I derive or use another equation for getting the acceration due to gravity for this? I don't know if I get that from a equation that I derive.
~Thanks~
Homework Statement
A ball is shot vertically upward from the surface of another planet.
A plot of y versus t for the ball is shown in the figure below, where y is the height of the ball above its starting point and t = 0 at the instance the ball is shot.
The figure’s vertical scale is set by ys = 30.0 m.
(a) Write expressions for the displacement and velocity of the ball as functions of time.
(b) What is the magnitude of the free-fall acceleration on the planet?
(c) What is the magnitude of the initial velocity of the ball?
~I've attatched a pic of the graph.
Homework Equations
I have to get the acceleration.
The Attempt at a Solution
a.) I need help on how to derive a equation from that graph and I don't know what the ys= 30m scale is that they describe.
I do know that since it is x vs. t graph I can get the v from that.
b.) would I solve the equation I derive or use another equation for getting the acceration due to gravity for this? I don't know if I get that from a equation that I derive.
~Thanks~