pizzamakeren
- 17
- 0
- Homework Statement
- I need help solving a problem related to acceleration.
- Relevant Equations
- The relevant equation will be postet as a picture below
The problem that i am facing has to do with acceleration. The problem states that we have two balls with the same mass m that stands on two different tables. Between these balls are a wire with the length 2l, which i assume means 2 * l, where l is a value i choose. In the middle of the wire (x = 0) a force F pulls down the rope.
The problem asks me to show that the following equation gives me the acceleration of m. It is also noted that we are going to ignore friction.
Now i am wondering if the solution to this is to plug in values for F, m and l that i choose for myself? Or is it more complicated than that?
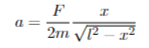
The problem asks me to show that the following equation gives me the acceleration of m. It is also noted that we are going to ignore friction.
Now i am wondering if the solution to this is to plug in values for F, m and l that i choose for myself? Or is it more complicated than that?