Ark236
- 24
- 3
- Homework Statement
- Hi everyone,
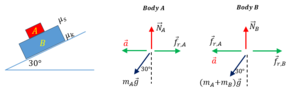
The problem consists of two stacked blocks, blocks A and B, that lie on an inclined plane at an angle theta. Block B is sliding on a rough surface whose static friction coefficient is muk. The block A is at rest over the block B, and between the surfaced of the blocks there is a static friction coefficient μs.
- Relevant Equations
- I want to determine the acceleration of each body (is the same). To do that, I determine the equation of motion for each body:
For the body B
sum fx^B: F_{r,B} - f_{r,A} - (m_A+m_B) g sin(theta) = - m_B a
sum fy^B: N_B - (m_A+m_B) g cos(theta) = 0
For the body A
sum fx^A: f_{r,A} - m_Ag sin(theta) = - m_A a
sum fy^A: N_A -m_A g cos(theta) = 0
In order to calculate the acceleration, I sum the equations sum fx^B and sum fx^A.
F_{r,B} - m_Ag sin(theta) - (m_A+m_B) g sin(theta) = - (m_A+m_B) a
then
a = -[F_{r,B} - (2 m_A+m_B) g sin(theta)]/(m_A+m_B)
=-[muk (m_A+m_B) g cos(theta) - (2 m_A+m_B) g sin(theta)]/(m_A+m_B)
but the correct answer is a = -[muk (m_A+m_B) g cos(theta) - (m_A+m_B) g sin(theta)]/(m_A+m_B). I don't know what my mistake is.
thanks
F_{r,B} - m_Ag sin(theta) - (m_A+m_B) g sin(theta) = - (m_A+m_B) a
then
a = -[F_{r,B} - (2 m_A+m_B) g sin(theta)]/(m_A+m_B)
=-[muk (m_A+m_B) g cos(theta) - (2 m_A+m_B) g sin(theta)]/(m_A+m_B)
but the correct answer is a = -[muk (m_A+m_B) g cos(theta) - (m_A+m_B) g sin(theta)]/(m_A+m_B). I don't know what my mistake is.
thanks