- #36
bob012345
Gold Member
- 2,133
- 941
As @hmmm27 said above you can use circles of different radii to adjust the bulge. I wasn't sure if the points are equidistant around the arc as drawn here but if not it is easy to adjust for that. But these are all circles with different centers so the equations are easy. The object comes in from the left at ##E## and leaves at ##F##.
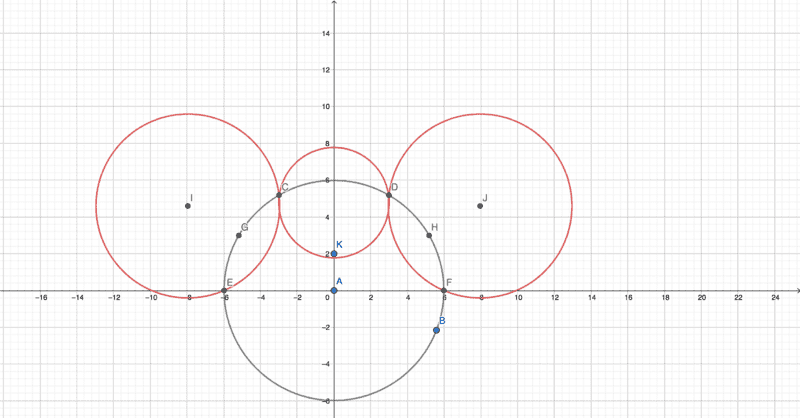
Update: I'm calling this the Mickey Mouse version...
Update: I'm calling this the Mickey Mouse version...
Last edited: