Acceleration-Time Graph and Velocity Multiple Choice Question

[AntSC]

Homework Statement

Finding $\Delta v$ from an $a-t$ graph

Relevant Equations

Area under graph methods

The variation with time t of the acceleration a of an object is shown

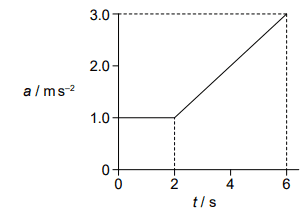
What is the change in velocity of the object from $t=0$ to $t=6$?

A. $6ms^{-1}$
B. $8ms^{-1}$
C. $10ms^{-1}$
D. $14ms^{-1}$

So apparently the answer is B, which I am having trouble reconciling.

Using methods of areas I get $2ms^{-1}$ for the first $2s$ and $8ms^{-1}$ for the last $4s$. Total $\Delta v=10ms^{-1}$ right?
I don't think there should be much more calculation needed for this question so I assume my interpretation is what is off.

I've tried doing this with calculus and I get the same answer, which isn't a surprise. I even tried assuming that $v=0$ at the start and built it up from there, which still gives me a $\Delta v$ of $10ms^{-1}$.

I'm a bit dumbfounded. Can anyone comment?

 

[BvU]

Hello,

Well, for what it's worth: I completely agree with you.
Here in PF we have often seen given answers to be mistaken and for now I assume that is the case here too !

$\$

 

[AntSC]

Hello,

Well, for what it's worth: I completely agree with you.
Here in PF we have often seen given answers to be mistaken and for now I assume that is the case here too !

$\$

Thanks BvU!
You've helped my sanity.
It's always uncertain with answers for multiple-choice questions as there's no working, so you can't retrace any steps.
Glad there's some agreement here

 

[kuruman]

Wait a minute. I am afraid this problem makes me question my sanity. The acceleration increases by 1 m/s² every 2 s. If it is 1 m/s² at $t= 2$ s, then it must be zero at $t=0$. The change in velocity $\Delta v$ from 0 s to 6 s is the area of the right triangle of base 6 s and height 3 m/s². This is 9 m/s.

Using calculus, $a=\frac {1}{2}t$. Then $$\Delta v= \frac {1}{2}\int_0^6t~dt=\left. \frac{1}{4}t^2 \right|_0^6= \frac{1}{4}\times (36-0) = 9~\text{m/s}$$Why is the correct answer 10 m/s? I don't believe that the correct answer is one of the given choices.

On edit: My sanity is restored. All of the above is incorrect but I need new glasses. See post #8.

 

[BvU]

then it must be zero at t=0.

The graph clearly shows an acceleration of 1 m/s² at t=0

$\$

 

[AntSC]

Wait a minute. I am afraid this problem makes me question my sanity. The acceleration increases by 1 m/s² every 2 s. If it is 1 m/s² at $t= 2$ s, then it must be zero at $t=0$. The change in velocity $\Delta v$ from 0 s to 6 s is the area of the right triangle of base 6 s and height 3 m/s². This is 9 m/s.

Using calculus, $a=\frac {1}{2}t$. Then $$\Delta v= \frac {1}{2}\int_0^6t~dt=\left. \frac{1}{4}t^2 \right|_0^6= \frac{1}{4}\times (36-0) = 9~\text{m/s}$$Why is the correct answer 10 m/s? I don't believe that the correct answer is one of the given choices.

But the acceleration function is a piecewise function and the $\frac{1}{4}t^2$ function you have used only applies in the $1\leq t\leq 6$ domain and not $0\leq t\leq 6$. I did test this with integration too and still got $10ms^{-1}$ but maybe check again if you have the inclination.

I am not saying the answer is $10ms^{-1}$, just that I don't see what else it could be. Perhaps we're all making errors in different places LOL

I'm sure we can crack this.

Also thought that I would add that this question is from an official international baccalaureate standard level exam paper. You would think the published answers would have been at least triple-checked but who knows.

 

[jbriggs444]

I'm sure we can crack this.

You have already done so. Your answer is right and the answer key is wrong. It is an important lesson to learn that sometimes one can be right and the authorities can be wrong. [Just don't let it go to your head].

My guess is that someone wanted the graph to depict an acceleration of zero for the first two seconds, did the calculation that way and never checked to see whether the graph agreed with the answer.

 

[kuruman]

The graph clearly shows an acceleration of 1 m/s² at t=0

$\$

Oops! My tired old eyes didn't discern that the horizontal line from {0,1} to {2,1} is not dashed like its vertical counterpart. I stand corrected.

 

[BvU]

It took me several looks as well ! And that the vertical scale steps are 1 and the horizontal ones 2 didn't help much either

Oh well, keeps us sharp, I suppose

$\$