Acceleration Time if Thrust is Variable (polynomial)?

[bestpa]

Hi Everyone;

I hope this is the right forum.

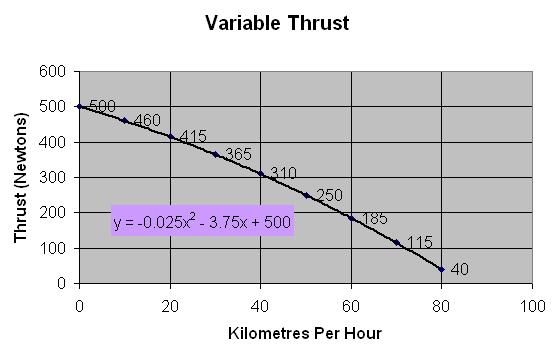
Here's the issue... with fixed pitch propeller aircraft, thrust is not a constant, and changes (among other variables) with the speed the aircraft is travelling. The thrust available can be calculated using a polynomial.

How do I integrate the polynomial into the acceleration equation?

Here is a simple example :

An aircraft weighing 4500N (1000lbs) accelerates to 60 Kilometres Per Hour. How long did that take?

Here is the data set:

Thrust(N)=-0.025x^2 - 3.75x + 500

KPH, Thrust(N)
0, 500
10, 460
20, 415
30, 365
40, 310
50, 250
60, 185
70, 115
80, 40

 

[Enthalpy]

Hi!

As air drag isn't mentioned, we'll neglect it... Sure it's false.

Thrust divided by mass gives you the acceleration. Integrate the acceleration (polynom) over time to get the speed over time.

Then, you'll have to integrate the time over each speed increment, from 0km/h to 60km/h (don't forget to convert to m/s) to get the elapsed time. Each time slice is the speed increment divided by the acceleration.

 

[bestpa]

Thanks for responding but I don't really understand what you are driving at...

The polynom describes the curve of available thrust over speed, but how do I integrate it into the equation? Can you write an equation for me?

Please tell me that you are not suggesting I "slice" up each velocity and perform the acceleration calculation for each "slice" ? This would be incorrect.

Please see the charts below that illustrate how inaccurate this method is. I'm sorry but I don't know how to format them for this site.

Example 1: "10 km/h slices"

m/s, KPH, Thrust(N), a = F / m, t=(V-Vo)/a
0.0 0 500 0.113636364 0
2.8 10 460 0.104545455 26.57004831
5.6 20 415 0.094318182 29.45113788
8.3 30 365 0.082954545 33.48554033
11.1 40 310 0.070454545 39.4265233
13.9 50 250 0.056818182 48.88888889
16.7 60 185 0.042045455 66.06606607
19.4 70 115 0.026136364 106.2801932
22.2 80 40 0.009090909 305.5555556

total seconds 655.7239536

Example 2: "5 km/h slices"

m/s, KPH, Thrust(N), a = F / m, t=(V-Vo)/a
0.0 0 500 0.113636364 0
1.4 5 480.625 0.109232955 12.71492559
2.8 10 460 0.104545455 13.28502415
4.2 15 438.125 0.099573864 13.94832779
5.6 20 415 0.094318182 14.72556894
6.9 25 390.625 0.088778409 15.64444444
8.3 30 365 0.082954545 16.74277017
9.7 35 338.125 0.076846591 18.07352639
11.1 40 310 0.070454545 19.71326165
12.5 45 280.625 0.063778409 21.77678792
13.9 50 250 0.056818182 24.44444444
15.3 55 218.125 0.049573864 28.01655524
16.7 60 185 0.042045455 33.03303303
18.1 65 150.625 0.034232955 40.57169202
19.4 70 115 0.026136364 53.14009662
20.8 75 78.125 0.017755682 78.22222222
22.2 80 40 0.009090909 152.7777778

total seconds 556.8304584

 

[Integral]

Seems to me that all you need do to get the acceleration at any velocity is divide by the mass.

a(v)= T(v)/M

Not sure what you are doing with the time slice stuff??

 

[Integral]

You can write the differential equation:

$$\dot {v} = \frac {T(v)} M$$

A simple method, but not the best way is use Eulers Method. For this:

$$v(t_{n+1}) = h * \frac {T(v(t_n))} M$$

where

$$t_{n+1} = t_{n} + h$$

h may need to be small.

 

[rcgldr]

Please tell me that you are not suggesting I "slice" up each time and perform the acceleration calculation for each "slice"?

Redo the tables using average thrust and acceleration (1/2 x (beginning + ending thrust)) for each velocity slice. As the slices get smaller, you should approach a fixed limit. A multi-step method like Runge-Kutta would also work.

 

[bestpa]

Thanks for replying everyone, just a couple of things:

I am looking to find the time to accelerate an object to a certain speed, where the thrust changes through the different velocities.

1) "Integral" thanks for your formulas, but I'm not trying to find the acceleration for a given velocity, I can get that by completing the polynomial listed in my chart. The purpose of my "time slice" experiment was to try and find the *total time* to accelerate from a certain speed to a certain speed (0-60kph). Your formulas seem to be based around "v", and velocity I already know. I see you are very active on this forum, and thank you nonetheless for your input.

2) Jeff.. .maybe you have something there with average aceleration... I never thought about that before!

Of course, I wonder if it's as simple as (1/2 x (beginning + ending thrust)). I can see it making sense if the beginning thrust and end thrust were connected on a "straight line", but i wonder about getting the average between two points on a non-linear curve described by this polynomial ...

Half the thrust between the two points of speed on that curve is not half the distance between the two points, therefore I need to explore the math involved to find the average of two points.

 

[Integral]

Note that the Euler method in my second post is in time steps. Run that routine until you reach the desired velocity.

The Runga Kutta method mentioned by DH is a better method then the Euler, but a little more difficult to explain and code. Do a web search there is lots of info about it out there.

 

[bestpa]

Thanks for you help everyone.

Well, it looks like I won't be able to get my mathematical shortcut, but by writing a quick program to calculate using a different number of slices of velocity each execution, I should be able to see if using the average thrust will provide a sufficiently accurate number.

After running it several times, I see that the difference between using 900 and 9000 slices is negligable, however, there is some difference between 8 and 9 and 90.

Below please find the perl script I made (released gratis) , the results after running numerous times, and the table redone with the average thrust of each "slice".

m/s ,KPH, Thrust(N), Ave Thrust, a = F / m, t=(V-Vo)/a
0.0 0 500 500 0.113636364 0
2.8 10 460 480 0.109090909 25.46296296
5.6 20 415 437.5 0.099431818 27.93650794
8.3 30 365 390 0.088636364 31.33903134
11.1 40 310 337.5 0.076704545 36.21399177
13.9 50 250 280 0.063636364 43.65079365
16.7 60 185 217.5 0.049431818 56.19412516
19.4 70 115 150 0.034090909 81.48148148
22.2 80 40 77.5 0.017613636 157.7060932

total seconds 459.9849875

As you can see, I used 8 steps above.

Here's the output of my perl script after 8 steps, then beyond. You can see the result work itself towards a finite number.

Slices : 8 , Time Calculated : 459.984987489931 seconds
Slices : 9 , Time Calculated : 462.490081272261 seconds
Slices : 90 , Time Calculated : 474.967386020087 seconds
Slices : 900 , Time Calculated : 475.139573557721 seconds
Slices : 9000 , Time Calculated : 475.14130515812 seconds
Slices : 90000 , Time Calculated : 475.141322475107 seconds
Slices : 900000 , Time Calculated : 475.14132264829 seconds
Slices : 9000000 , Time Calculated : 475.141322649987 seconds Good enough for me!Here's the code:

#/usr/bin/perl
# PB Freeware, use, abuse.

$kphfinal=80;
$mass=4400;

$velocityslices=900000;

#print "VelocitySlices: $velocityslices \n";

$step=1;
$timetotal=0;

$thrustlast=500;
$kphlast=0;

while ($step<=$velocityslices) {

$kph=$kphfinal/$velocityslices*$step;
#print "kph now: $kph \t ";

$thrustnow=-0.025*($kph**2)-3.75*$kph+500;
#print "thrust now: $thrustnow N\t";
$thrustaverage=0.5*($thrustnow+$thrustlast);
#print "ave. thrust $thrustaverage N \t";

$accel=$thrustaverage/$mass;
#print "Acceleration : $accel m/s^2 \n";

$timethisstep=($kph/60/60*1000-$kphlast/60/60*1000)/$accel;
#print "Time this step : $timethisstep seconds \n";

$timetotal=$timetotal+$timethisstep;

$kphlast=$kph;
$thrustlast=$thrustnow;

$step++;
};print "Slices : $velocityslices , Time Calculated : \t $timetotal seconds \n";​

 

[rcgldr]

Jeff.. .maybe you have something there with average aceleration... I never thought about that before!

This is just linear interpolation, assuming that the rate of change between small steps is linear. You could also do two sets of calculations, one using beginning thrust per step, the other using the ending thrust per step, and note that their sums approach a common limit as the step size gets smaller.

You could also use the derivative of the thrust versus velocity function, and use the velocity where the slope of the derivative equals the slope from the beginning and end points, and base the thrust on this velocity, but as the steps get small enough the linear method should work because the function is smooth enough.

It's also possible to run into truncation issues. I don't know if it's possible to select between float and double in perl, but if it is, use double. You can also use a function to sum a very large number of very small numbers, that uses a table indexed by the exponent of the numbers in the table (it's initialized to zero), then do a final summation of all the numbers in that table.

 

[bestpa]

Hey Jeff, how inaccurate do you think my method was? Do you really think we're talking about more than 10 second +/- difference with more advanced calculation techniques? I'm just going to use the method to eventually determine things like range, and runway needed until rotation (take off) for an aircraft design.

I've got to tell you that with the accuracy required for the initial sizing, if I'm splitting hairs and 10 seconds over that whole acceleration really means a difference to me, ... I'm probably just setting myself up to die in the thing!

As a ballpark figure stands, do you think I am I out by more than a percent? I don't.

 

[nasu]

If you know the expression for trust versus velocity, you can solve the problem directly.
You write the equation
a=dv/dt = av^2+bv+c
And solve it to get v as a function of t.
You'll have dt=dv/(av^2+b*v+v) and integrate both sides.
You'll get t as a function of v and then you solve the equation to get v as a function of t or just tabulate the function.

 

[rcgldr]

Hey Jeff, how inaccurate do you think my method was? As a ballpark figure stands, do you think I am I out by more than a percent? I don't.

I don't know. Making two programs, one that uses the largest (beginning) thrust and the other using the smallest (ending) thrust, and verifying that they both converge towards the same number as the number of samples increases would help.

Since this is a non-alternating series, the truncation issue should show up as the total time slightly decreasing as the steps get smaller since the total time is based on the sum of many small values.

It's possible that you can directly integrate this as pointed out by nasu, but once you include other factors like aerodynamic drag, then you're stuck with numerical integration.

 

[bestpa]

Perl stores every number as a double, so I'm not worried about truncation.

Here is the output using the lower acceleration (starting acceleration) within the speed slice of velocity:

Slices : 9 , Time Calculated : 382.788798144722 seconds
Slices : 90 , Time Calculated : 463.034913978877 seconds
Slices : 900 , Time Calculated : 473.895825777039 seconds
Slices : 9000 , Time Calculated : 475.016423238041 seconds
Slices : 90000 , Time Calculated : 475.128829211472 seconds
Slices : 900000 , Time Calculated : 475.140073271188 seconds

Here, again, is the output using the median (in the middle of the highest and lowest m/s^2) acceleration within the speed slice of velocity:

Slices : 9 , Time Calculated : 462.490081272261 seconds
Slices : 90 , Time Calculated : 474.967386020087 seconds
Slices : 900 , Time Calculated : 475.139573557721 seconds
Slices : 9000 , Time Calculated : 475.14130515812 seconds
Slices : 90000 , Time Calculated : 475.141322475107 seconds
Slices : 900000 , Time Calculated : 475.14132264829 seconds Here is the output using the highest acceleration (ending acceleration) within the speed slice of velocity:

Slices : 9 , Time Calculated : 632.665341354598 seconds
Slices : 90 , Time Calculated : 488.022568299865 seconds
Slices : 900 , Time Calculated : 476.394591209138 seconds
Slices : 9000 , Time Calculated : 475.26629978125 seconds
Slices : 90000 , Time Calculated : 475.153816865792 seconds
Slices : 900000 , Time Calculated : 475.14257203663 seconds

Given that using the acceleration is known to be too low, and the highest acceleration is known to be too high, the number must be somewhere in between them.

After calculating using the most slices (900000) , the results that are close to the finite number are :

LOW : Slices : 900000 , Time Calculated : 475.140073271188 seconds
MED : Slices : 900000 , Time Calculated : 475.14132264829 seconds
HIGH: Slices : 900000 , Time Calculated : 475.14257203663 seconds

This shows a difference of less than 3/1000's of a second over 475 seconds, so I'm really not too worried unless there is a fundamental flaw with using interpolation in this way.

 

[rcgldr]

LOW : Slices : 900000 , Time Calculated : 475.140073271188 seconds
MED : Slices : 900000 , Time Calculated : 475.14132264829 seconds
HIGH: Slices : 900000 , Time Calculated : 475.14257203663 seconds

You've got low and high reversed (higher acceleration is lower time), but you see the point here, as the steps get higher, the numbers converge. This same logic applies to the fundamental theorem of calculus, as the step size approaches zero, and the number of steps approaches infinity, it doesn't matter what point in each interval you choose, the limit will have the same value (assuming the function is continuous).

Still you're ignoring some other variables here, (rolling resistance, aerodynamic drag, prop advance affects), so real world testing is still needed.

 

[bestpa]

I wasn't after things like drag, lift, prop effeciency, etc. Only acceleration. I feel confident that I have the answers I was looking for - this time!

For the rest, I intend on integrating different polynomials. That's an issue for a different day!

Thanks to all who responded.

 

[bestpa]

Also, disclaimer, in no way is the number set I chose for acceleration real-world. An aircraft weighing 1000lbs taking 8 minutes to reach 80mph... I don't really think there's enough pavement ! ;)