- #1
Saitama
- 4,243
- 93
Homework Statement
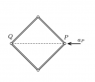
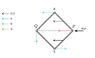
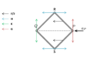
Four similar rods of uniform density are connected with frictionless hinges, and this frame is placed to a horizontal smooth tabletop, such that its shape is a square. Vertex P is acted upon by a horizontal force in the direction of the diagonal, and due to this force it begins to move at an acceleration of aP. What is the acceleration of the opposite vertex Q at which it begins to move?
Homework Equations
The Attempt at a Solution
I have no idea how to begin with this question. I can't visualize how the body would move when only one one of the vetex is given an acceleration.
Any help is appreciated. Thanks!