FoggyNight
- 2
- 0
Acoustic Wave Velocities in Brillouin Zone - Phonon Spectrum of Ge
Acoustic Wave Velocities in Brillouin Zone - Phonon Spectrum Diagram
The exact problem I'm stuck on is Q3c on this exam paper. I have included an image of the problem below. I haven't
had any trouble up to this point, but I'm stuck on the second half of this part of this question.
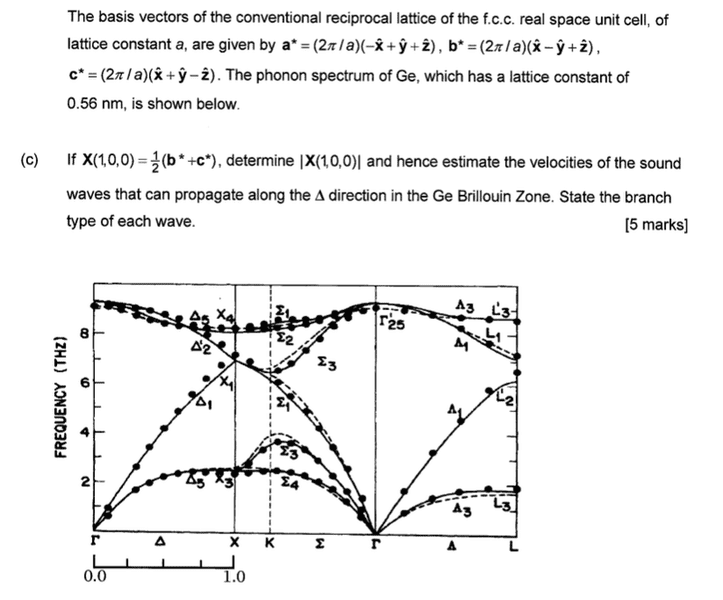
The question gives the phonon spectrum of germanium as well as information about Ge (listed below) and then asks me to calculate |X(1,0,0)| (which I've done) and to hence estimate the velocities of the sound waves that can propagate along the Δ direction in the Ge Brillouin Zone. I also have to state the branch type of each wave, which I understand.
a*=(2π/a)(-x^+y^+z^), b*=(2π/a)(x^-y^+z^), c*=(2π/a)(x^+y^-z^)
Lattice constant = 0.56nm
X(1,0,0)=1/2(b*+c*)
ω=2πf
v=ω/k
So I can calculate |X(1,0,0)| as follows:
X(1,0,0)=1/2(b*+c*)=(2π/a)x^
|X(1,0,0)|=(2π/a)√(1^2)=2π/a=1.12x10^10 m^-1
This is where I get confused: I'm able to identify the 2TA waves and the LA wave, however,
I'm not sure exactly what values to sub into the ω=2πf and v=ω/k equations.
For the frequency do I just come directly up from the first delta on the x-axis and when I hit
a wave take the frequency at that point? I.e. LA would be ~4 and the degenerate TAs would
be ~2. We have the k for X(1,0,0) as 1.12x10^10m^-1, so would the lambda k be half this
value? Any advice on how to proceed would be greatly appreciated. Thanks for reading.
Homework Statement
Acoustic Wave Velocities in Brillouin Zone - Phonon Spectrum Diagram
The exact problem I'm stuck on is Q3c on this exam paper. I have included an image of the problem below. I haven't
had any trouble up to this point, but I'm stuck on the second half of this part of this question.
The question gives the phonon spectrum of germanium as well as information about Ge (listed below) and then asks me to calculate |X(1,0,0)| (which I've done) and to hence estimate the velocities of the sound waves that can propagate along the Δ direction in the Ge Brillouin Zone. I also have to state the branch type of each wave, which I understand.
Homework Equations
a*=(2π/a)(-x^+y^+z^), b*=(2π/a)(x^-y^+z^), c*=(2π/a)(x^+y^-z^)
Lattice constant = 0.56nm
X(1,0,0)=1/2(b*+c*)
ω=2πf
v=ω/k
The Attempt at a Solution
So I can calculate |X(1,0,0)| as follows:
X(1,0,0)=1/2(b*+c*)=(2π/a)x^
|X(1,0,0)|=(2π/a)√(1^2)=2π/a=1.12x10^10 m^-1
This is where I get confused: I'm able to identify the 2TA waves and the LA wave, however,
I'm not sure exactly what values to sub into the ω=2πf and v=ω/k equations.
For the frequency do I just come directly up from the first delta on the x-axis and when I hit
a wave take the frequency at that point? I.e. LA would be ~4 and the degenerate TAs would
be ~2. We have the k for X(1,0,0) as 1.12x10^10m^-1, so would the lambda k be half this
value? Any advice on how to proceed would be greatly appreciated. Thanks for reading.
Last edited: