Adding trig functions with different amplitudes

[Mayhem]

TL;DR

A general rule for adding two trigonometric functions that have unidentical amplitudes

The trig identities for adding trig functions can be seen:

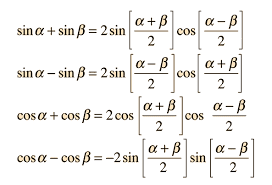
But here the amplitudes are identical (i.e. A = 1). However, what do I do if I have two arbitrary, real amplitudes for each term? How would the identity change?

Analysis: If the amplitudes do show up on the RHS, we would expect them to either be a product or sum of these, possibly signed, or simply explicitly states. For A = 1, it may be difficult to see where they appear if explicitly stated, as they disappear as a factor. However, what we do see is that 2 appears in front of all of the RHS identities, which is a hint that for A_1 = A_2 = 1, we simply add them together and place them as a factor in front of the expression. However, this isn't necessarily the case, and simply and intuition, and considering 2 also appears in the denominators of the inner terms, it isn't a given that the number 2 shows up for this reason.

I don't know the derivations of the above identities, so I'm wondering if there is a way to generalize something like Asin(a) + Bsin(b) such that these terms are accounted for on the RHS of an equivalent expression.

 

[FactChecker]

There is no general simplification for that situation. You just have to leave them as the multiplied sum of two different trig functions.

 

[Mayhem]

There is no general simplification for that situation. You just have to leave them as the multiplied sum of two different trig functions.

Well that's annoying. The problem is I am trying to program a Fourier transform, which requires me to make a linear combination of trig functions. However, I can probably figure out a workaround.

 

[FactChecker]

Well that's annoying. The problem is I am trying to program a Fourier transform, which requires me to make a linear combination of trig functions. However, I can probably figure out a workaround.

If your program only has to calculate a linear combination of a couple of trig functions, then a computer can easily do the calculation directly.
If you are trying to calculate the Fourier transform of a general function and have enough data points, then you should look into the Fast Fourier Transformation (FFT). There are several implementations of the FFT algorithm. (see https://en.wikipedia.org/wiki/Fast_Fourier_transform)

 

[pasmith]

These identities are derived from $$\begin{split} \cos(a \pm b) &= \cos a \cos b \mp \sin a \sin b, \\<br /> \sin(a \pm b) &= \sin a \cos b \pm \cos a \sin b. \end{split}$$ Their purpose in the context of transforms is to turn products into sums. For example $$\begin{split}<br /> \left(\sum_{n=0}^N a_n \cos(nx)\right)\left(\sum_{n=0}^N b_n \cos(nx)\right)<br /> &= \sum_{n=0}^N \sum_{m=0}^N a_n b_m \cos (nx) \cos(m x) \\<br /> &= \frac12 \sum_{n=0}^N \sum_{m=0}^N<br /> a_nb_m \left( \cos((n+m)x) + \cos((n-m)x)\right)\end{split}$$ and from there you can work out which values of $n$ and $m$ will contribute to the coefficients $c_r$ in $\sum_{r=0}^N c_r \cos(rx)$.

You can use these identities to do what you were originally attempting, but it is unclear to me why you would want to write $(A + B)\sin((a+b)/2)\cos((a-b)/2) + (A - B)\cos((a+b)/2)\sin((a-b)/2)$ instead of $A \sin a + B \sin b$.

 

[Svein]

Have you tried the inverse Fourier transform? https://en.wikipedia.org/wiki/Fourier_inversion_theorem.