pairofstrings
- 411
- 7
- TL;DR Summary
- How do I add x + xy =1?
Hello.
How do I add 'x' to 'xy', and the resultant should be <= 1?
x + xy = 1
PEMDAS:
Step 1: Multiply 'x' and 'y' (2nd term in the equation)
Step 2: Add 1st term to 2nd term of the equation
Step 1 plus Step 2 should yield value <=1.
I know that the curve look like this:
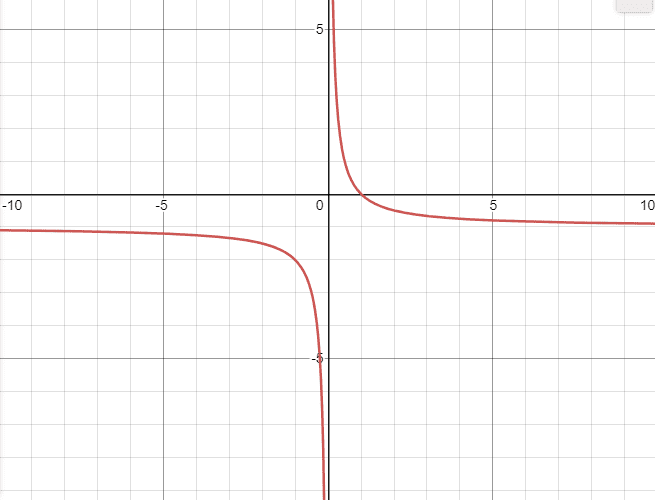
'xy' will give me a curve to which I need to add 'x' and this graph is the output after I add 'x' to equation:
x + xy = 1.
How do I get the resultant without simplifying like the following:
x + xy = 1
x (1 + y) = 1 ;
1 + y = 1/x
Then I could plug in numbers into 'x' to get y..
Table:
x | y
1 0
Thanks.
How do I add 'x' to 'xy', and the resultant should be <= 1?
x + xy = 1
PEMDAS:
Step 1: Multiply 'x' and 'y' (2nd term in the equation)
Step 2: Add 1st term to 2nd term of the equation
Step 1 plus Step 2 should yield value <=1.
I know that the curve look like this:
'xy' will give me a curve to which I need to add 'x' and this graph is the output after I add 'x' to equation:
x + xy = 1.
How do I get the resultant without simplifying like the following:
x + xy = 1
x (1 + y) = 1 ;
1 + y = 1/x
Then I could plug in numbers into 'x' to get y..
Table:
x | y
1 0
Thanks.