Advanced problem on Kinetic Theory of Gases

[zorro]

Homework Statement

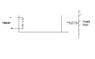
An ideal monoatomic gas is confined in a cylinder by a spring-loaded piston of cross section 8 x 10^-3m². Initially the gas is at 300K and occupies a volume of 2.4 x 10^-3 m³ and the spring is in its relaxed state. The gas is heated by a smalll heater until the piston moves out slowly by 0.1 m. Calculate the final temp of the gas. The force constant of the spring equals 8000N/m, Patm = 1atm. The cylinder and the piston are thermally insulated. The piston and the spring are massless and there is no friction between the piston and the cylinder. Neglect any heat loss through lead wires of the heater. The heat capacity of the heater coil is negligible.

The Attempt at a Solution

Work done by the gas in expansion
W = 0.5kx² + Patm x A x 0.1
Since the cylinder and piston are thermally insulated.
Work done equals the change in internal energy i.e. W=nCv\DeltaT

on solving, nCv\DeltaT = 120
now Cv=1.5R and n=PV/RT
so 1.5PV\DeltaT/T = 120
P,V,T are known to us
so \DeltaT = 100
T₂ - T=100
T₂=100 + 300 =400

But the answer is 800 K which only differs by a factor of 2.
Please tell me what is the problem.
I checked all my calculations. They are correct.

 

[Andrew Mason]

You are assuming this is adiabatic? The question says the gas is heated. So \Delta Q \ne 0. Apply the first law. Work done by the gas does not equal (-) change in internal energy.

I don't think you need to find the work done. What you have to do is apply the ideal gas law to find the final state (Pf, Vf, Tf). But to do that, you need to know the final pressure. Work that out. When you get that, you will be able to find the final temperature.

AM

 

[zorro]

Thanks a lot Sir!
I got my answer.