mcastillo356
Gold Member
- 639
- 348
- TL;DR Summary
- I'm familiar to this ground, but the function composition I introduce is difficult for me
Hi PF
I have a quote from Spanish 6th edition of "Calculus", by Robert A. Adams, and some queries. I translate it this way:"The inverse of secondary trigonometric functions can easily be calculated with the reciprocal function. For example
DEFINITION 13 The inverse function of secant ##sec^{-1} x## (or ##\mbox{arcsec}x##)
$$sec^{-1}=cos^{-1}\left({\dfrac{1}{x}}\right)\quad for\;|x|\geq 1$$
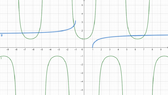
The domain of ##\sec^{-1}## is the union of intervals ##(-\infty,-1]\cup{[1,\infty)}## and ##[0,\dfrac{\pi}{2})\cup{(\dfrac{\pi}{2},\pi)}##. The graph of ##y=sec^{-1}x## is shown in Figure 3.25(b)(*). Is the reflection respect to the line ##y=x## of the part of ##\sec x## for ##x## between 0 and ##\pi##. Additionally
$$\sec(\sec^{-1}x)=\sec\left({\cos^{-1}\left({\dfrac{1}{x}}\right)}\right)
=\dfrac{1}{\cos\left({\cos^{-1}\left({\dfrac{1}{x}}\right)}\right)}=\dfrac{1}{\dfrac{1}{x}}=x\qquad{\mbox{for}\;|x|\geq 1}$$Up to now I've got to deal only with very easy compound functions. This quote represents a qualitative step forward. The domains and ranges are shown, but I would like to know: what if I had to do it by myself, if I was given only the identities, and had to manage to describe the domain and range of, suppose, the one at DEFINITION 13?
$$cos^{-1}\left({\dfrac{1}{x}}\right)$$
With no other help but the knowledge of the domain of ##y=\mbox{arcos}(x)##, ##(-1\leq x\leq 1)##, and ##\mathbb{R}\setminus{\{0\}}## for ##\dfrac{1}{x}##
As well, isn't there a mistake, a typo, at the sentence "Is the reflection respect to the line ##y=x## of the part of ##\sec x## for ##x## between 0 and ##\pi##"? Shouldn't be "of the part of ##sec^{-1} x##"?.
(*)Attached image
Attempt: Pure speculation; don't know why, but I've come across this statement: domain shouldn't be the intersection of the domain of ##y=\cos x## and the domain of the inverse function of ##y=\dfrac{1}{x}##?
I have a quote from Spanish 6th edition of "Calculus", by Robert A. Adams, and some queries. I translate it this way:"The inverse of secondary trigonometric functions can easily be calculated with the reciprocal function. For example
DEFINITION 13 The inverse function of secant ##sec^{-1} x## (or ##\mbox{arcsec}x##)
$$sec^{-1}=cos^{-1}\left({\dfrac{1}{x}}\right)\quad for\;|x|\geq 1$$
The domain of ##\sec^{-1}## is the union of intervals ##(-\infty,-1]\cup{[1,\infty)}## and ##[0,\dfrac{\pi}{2})\cup{(\dfrac{\pi}{2},\pi)}##. The graph of ##y=sec^{-1}x## is shown in Figure 3.25(b)(*). Is the reflection respect to the line ##y=x## of the part of ##\sec x## for ##x## between 0 and ##\pi##. Additionally
$$\sec(\sec^{-1}x)=\sec\left({\cos^{-1}\left({\dfrac{1}{x}}\right)}\right)
=\dfrac{1}{\cos\left({\cos^{-1}\left({\dfrac{1}{x}}\right)}\right)}=\dfrac{1}{\dfrac{1}{x}}=x\qquad{\mbox{for}\;|x|\geq 1}$$Up to now I've got to deal only with very easy compound functions. This quote represents a qualitative step forward. The domains and ranges are shown, but I would like to know: what if I had to do it by myself, if I was given only the identities, and had to manage to describe the domain and range of, suppose, the one at DEFINITION 13?
$$cos^{-1}\left({\dfrac{1}{x}}\right)$$
With no other help but the knowledge of the domain of ##y=\mbox{arcos}(x)##, ##(-1\leq x\leq 1)##, and ##\mathbb{R}\setminus{\{0\}}## for ##\dfrac{1}{x}##
As well, isn't there a mistake, a typo, at the sentence "Is the reflection respect to the line ##y=x## of the part of ##\sec x## for ##x## between 0 and ##\pi##"? Shouldn't be "of the part of ##sec^{-1} x##"?.
(*)Attached image
Attempt: Pure speculation; don't know why, but I've come across this statement: domain shouldn't be the intersection of the domain of ##y=\cos x## and the domain of the inverse function of ##y=\dfrac{1}{x}##?
Attachments
Last edited by a moderator: