After entanglement swapping, how can we verify the new entanglement?

[r20]

TL;DR Summary

After entanglement swapping, how can we verify the new entanglement exists?

Suppose photons 1 and 2 have entangled spins. And, so do 3 and 4. A Bell-state measurement (BSM) is performed on photons 2 and 3 to cause entanglement swapping so 1 and 4 are now entangled. This is done many times creating many 1 and 4 pairs.

Suppose the original 1s and 2s were prepared such that they had opposite spins, and like wise the 3s and 4s. When entanglement is swapped, it is my understanding that some 1s and 4s would show the same spin if measured in the same direction and some would show opposite spin if measured in the same direction.Since this is different than having pairs all entangled in opposite directions, I'm wondering how we can determine if the 1s and 4s are entangled?

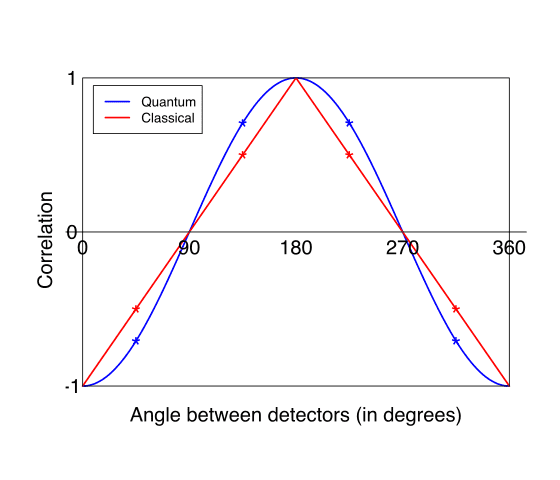
If the pairs all had opposite directions, I'd expect we could use Bell inequality. We'd measure the 1s in one direction and the 4s in other directions and plot the correlation graph and it would follow this:

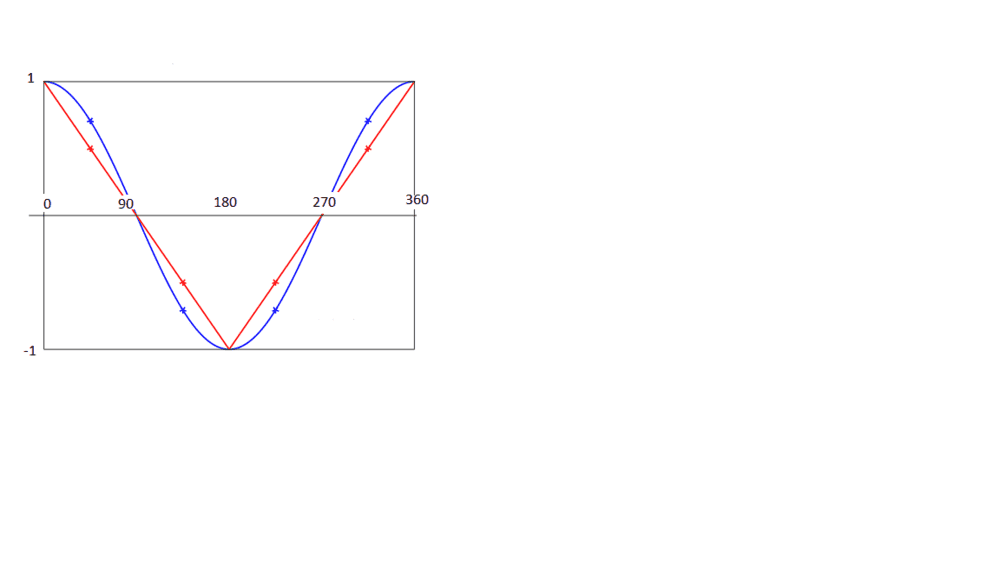
However, those that had spins in the same direction would fit the inverse of that graph:

Since we'd have some of each for swapped entanglement, average results would be a wash.

So, how can we determine whether the 1s and 4s are entangled? It must require knowledge from their former 2 and 3 pairs, right?

 

[DrChinese]

So, how can we determine whether the 1s and 4s are entangled? It must require knowledge from their former 2 and 3 pairs, right?

Good question!

The initial entanglement (1 & 2) and (3 & 4) must be known as being same or opposite spins (polarization). So you are correct about that.

When the swap occurs, Bell State Measurement (BSM) is made as you mention. The apparatus is, by convention, called a Bell State Analyzer (BSA). The outcome of the BSM can be any of 4 entangled states (or no entanglement at all, which is the most common outcome - but let's ignore these cases). You need to know which entangled state is created so you can properly interpret the results of your Bell test on photon pairs 1 & 4. Sometimes the 1 & 4 will be same spins, other times opposites, and they occur randomly.

It is interesting to note that the time ordering of the detections/measurements has no apparent effect on the results. This is of course completely consistent with quantum expectations. Check out Fig. 1 of the below reference. Note that they also perform a test to show HOM interference as part of the process, which also demonstrates entanglement was achieved. This paper is from a team led by Anton Zeilinger. It shows entanglement between photons were created from fully independent sources. Pretty amazing stuff.

https://arxiv.org/abs/0809.3991

 

[James2018]

Each photon is in a superposition of different polarizations. Measured together, they are in a superposition of being in identical polarizations and of different polarizations.
EDIT: mixture of different polarizations because the superposition of each single photon decoheres by being coupled to the superposition of the partner photon from the entangled pair by the means of angular momentum conservation (circular polarization is the angular momentum of the photon).

If the photons have identical frequencies and polarizations they exit on the same output port of the beam splitter due to the Hong ou Mandel effect (bosonic statistics) creating the phi states. If they do not have identical frequencies and polarizations they exit either on the same (psi+) or on different output ports (psi-) with equal probability. Only the case where they exit on different output ports can be distinguished by coincidence counting (each photon hits a different detector).

That is how entanglement swapping of independent photons from different polarization entangled pairs occurs.

In the link posted above by DrChinese, the polarizing beam splitters further help distinguish between psi+ and psi- in the case the photons have different polarizations.

 

[vanhees71]

It's important to note that in an entangled photon pair the single photons are not in a superposition of polarizations but in a mixed state. E.g., for the singlet state (a maximally entangled state), $|\Psi \rangle=1/\sqrt{2}(|HV \rangle-|VH \rangle)$ the single-photon polarization state for both photons is described by $\hat{\rho}=1/2 \hat{1}$. It is calculated as the partial trace of $|\Psi \rangle \langle \Psi|$, "tracing out one photon".

 

[James2018]

It's important to note that in an entangled photon pair the single photons are not in a superposition of polarizations but in a mixed state. E.g., for the singlet state (a maximally entangled state), $|\Psi \rangle=1/\sqrt{2}(|HV \rangle-|VH \rangle)$ the single-photon polarization state for both photons is described by $\hat{\rho}=1/2 \hat{1}$. It is calculated as the partial trace of $|\Psi \rangle \langle \Psi|$, "tracing out one photon".

I remember that. Thanks for mentioning. Which means the photons from independent pairs are in a mixture of entangled states that are distinguished by HOM interference and polarization-splitting measurements.

 

[vanhees71]

They are in a mixture. You can not empirically check whether the single photon at one place is entangled with another by just measuring something on this one photon. You have to measure something on both photons (and making sure that you do the measurement on the entangled pair, which can be achieved by coincidence measurements on the two photons you know or expect to be entangled). To fully determine the state you have to do various measurements on ensembles of equally prepaired photon pairs, e.g., measurements of their polarization in various (relative) directions.