MHB Ale's question at Yahoo Answers regarding a tunnel with parabolic cross-section

[MarkFL]

Here is the question:

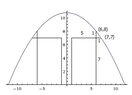
This is another question about parabola?

This is another question about parabola.

A tunnel is to built to allow 2 lanes of traffic to pass from one side of a mountain to the other side. The largest vehicles are trucks, which can be considered as rectangles 5m wide and 7m high.
Investigate the cross-section of a parabolic tunnel and find a possible equation to represent it. Allow some space so trucks do not bump into each other or the sides of the tunnel.

Here is a link to the question:

This is another question about parabola? - Yahoo! Answers

I have posted a link there so the OP can find my response.

 

[MarkFL]

Re: ale's question at Yahoo! Ansers regarding a tunnel with parabolilc cross-section

Hello ale,

Let's orient the origin of our coordinate system such that it is at the mid-point of the base of the cross-section, with the vertex of the parabola directly above it.

Let's allow 1 m on either side of the trucks and above them as in the diagram:

https://www.physicsforums.com/attachments/832._xfImport

We see we will require the parabola to pass through the points:

$$(\pm6,8),\,(\pm7,7)$$

Now, letting the parabola be:

$$P(x)=ax^2+bx+c$$

we obtain the linear system:

(1) $$P(6)=36a+6b+c=8$$

(2) $$P(-6)=36a-6b+c=8$$

(3) $$P(7)=49a+7b+c=7$$

(4) $$P(-7)=49a-7b+c=7$$

Adding (1) and (2) and (3) and (4) to eliminate $b$, we get:

(5) $$36a+c=8$$

(6) $$49a+c=7$$

Subtracting the (5) from (6) to eliminate $c$, we find:

$$13a=-1\,\therefore\,a=-\frac{1}{13}$$

and so substituting into (5), we have:

$$36\left(-\frac{1}{13} \right)+c=8\,\therefore\,c=\frac{140}{13}$$

and then substituting into (1) to find $b$, we get:

$$36\left(-\frac{1}{13} \right)+6b+8+36\left(\frac{1}{13} \right)=8\,\therefore\,b=0$$

And so we have found:

$$P(x)=-\frac{1}{13}x^2+\frac{140}{13}=\frac{140-x^2}{13}$$

To ale and any other guests viewing this topic, I invite and encourage you to post other algebra problems here in our http://www.mathhelpboards.com/f2/ forum.

Best Regards,

Mark.

 

[Alelin]

Re: ale's question at Yahoo! Ansers regarding a tunnel with parabolilc cross-section

Hello ale,

Let's orient the origin of our coordinate system such that it is at the mid-point of the base of the cross-section, with the vertex of the parabola directly above it.

Let's allow 1 m on either side of the trucks and above them as in the diagram:

View attachment 832

We see we will require the parabola to pass through the points:

$$(\pm6,8),\,(\pm7,7)$$

Now, letting the parabola be:

$$P(x)=ax^2+bx+c$$

we obtain the linear system:

(1) $$P(6)=36a+6b+c=8$$

(2) $$P(-6)=36a-6b+c=8$$

(3) $$P(7)=49a+7b+c=7$$

(4) $$P(-7)=49a-7b+c=7$$

Adding (1) and (2) and (3) and (4) to eliminate $b$, we get:

(5) $$36a+c=8$$

(6) $$49a+c=7$$

Subtracting the (5) from (6) to eliminate $c$, we find:

$$13a=-1\,\therefore\,a=-\frac{1}{13}$$

and so substituting into (5), we have:

$$36\left(-\frac{1}{13} \right)+c=8\,\therefore\,c=\frac{140}{13}$$

and then substituting into (1) to find $b$, we get:

$$36\left(-\frac{1}{13} \right)+6b+8+36\left(\frac{1}{13} \right)=8\,\therefore\,b=0$$

And so we have found:

$$P(x)=-\frac{1}{13}x^2+\frac{140}{13}=\frac{140-x^2}{13}$$

To ale and any other guests viewing this topic, I invite and encourage you to post other algebra problems here in our http://www.mathhelpboards.com/f2/ forum.

Best Regards,

Mark.

thank u :D