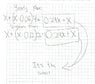Algebra, percentages bank interest problem (simple)

[Femme_physics]

Well, it seems simple, anyway, but I'm not sure why my methodology would be wrong.

Homework Statement

In a certain bank they offer 2 saving accounts.

Plan A gives an annual interest of 6%
Plan B gives an interest of 12% once every 2 year.

What's the preferable plan if you want to invest money for 4 years? Explain.

The Attempt at a Solution

Attached. X is defined as "original amount".

 

[Amok]

I'm not sure how banks work, but I think that in this case, after a year you'll get 6% of X and then the next years you'll get 6% of (6% of X + X). I think this is called compound interest, but I'm not sure this is the case with your problem.

 

[Femme_physics]

I'm not sure how banks work, but I think that in this case, after a year you'll get 6% of X and then the next years you'll get 6% of (6% of X + X). I think this is called compound interest, but I'm not sure this is the case with your problem.

Well, it must be the case since mine is not the right answer. I'll try it your way. Thanks :)

 

[eumyang]

I think you have to use the compound interest formula
A(t) = A_0 \left(1 + \frac{r}{n} \right)^{nt}
where
A₀ = the principal
t = time in years
n = number of compounding periods per year (monthly: n = 12; quarterly: n = 4...)
r = interest rate expressed as a decimal

Have you seen this equation before?

 

[Femme_physics]

I just used the long route to get to the solution. (attached)

Good thing they didn't ask for the next 2000 years or I'll have been writing it till next week...

But yea, it's best I use this formula next time. I think I've seen it before, but I haven't applied it. I really should, to save time. Thanks.