Algorithm for finding all the borders of R in all dimensions?

[esis]

Hey Guys!

To begin with, I apologize if I am using the wrong terminology. I've just begun learning about linear algebra.

So I was working on a problem in the book "Introduction to Linear Algebra" by Gilbert Strang, fourth edition (problems 9 and 11 on p. 8).

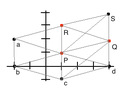
Problem 9: If three corners of a parallelogram are (1 , 1), (4, 2), and (1, 3), what are all three of the possible fourth corners? Draw Two of them.

Problem 11: Four corners of the cube are (0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1). What are the other four corners? Find the coordinates of the center point of the cube.

I solved these by drawing diagrams and identifying where to place the missing points, but this got me thinking of non-visual ways of solving the problem (if if you know of such a method, please let me know!)

How do you identify the vectors that delimit the span of a particular line(?)/plane(?)/Cube(?) etc. without actually visualizing the space?

I figured this algorithm might do the job:

#1 Start with all points equal to 1.
#2 Set the first component to zero.
#3 Move the zero, step by step, through all the components of the matrice until you reach the last component.
#4 Let the last component remain = 0, and set the first component to zero.
#5 Repeat #3 until you reach the component before the last zeroed component.
#6 Repeat until all component are zero
You now have all the borders of the space in any dimension.

i.e.
Dimension: 1, 2, 3, 4, 5, 6, 7 ...
Space A = (1, 1, 1, 1, 1, 1, 1, ...)

A1:
(1)
(0)

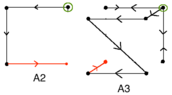
A2:
(1, 1)
(0, 1)
(0, 0)

A3:
(1, 1, 1)
(0, 1, 1)
(1, 0, 1)
(1, 1, 0)
(0, 1, 0)
(1, 0, 0)
(0, 0, 0)

(0, 0, 1)

A4:
(1, 1, 1, 1)
(0, 1, 1, 1)
(1, 0, 1, 1)
(1, 1, 0, 1)
(1, 1, 1, 0)
(0, 1, 1, 0)
(1, 0, 1, 0)
(1, 1, 0, 0)
(0, 1, 0, 0)
(1, 0, 0, 0)
(0, 0, 0, 0)

(0, 0, 0, 1)
(0, 0, 1, 1)

I figured I could use this to somehow solve problems 9 and 11 above... I'll continue working on this problem tonight, but do you think I am on the right track? I figured maybe I could use this algorithm to derive all the necessary points knowing only a single point and the dimension of the space. Again, I'm a complete newb just paying around, it would be interesting to hear your thoughts :)

EDIT: I just realized that for this to work, the algorithm needs be run backwards for dimensions over two! It will need 1 run for A3, two for A4... and hmm, I wonder how many for A5...?

 

[Deveno]

For a parallelogram, PQRS, we have 2 parallel sides, so (for example) if we have P,Q,R so that we have two vectors PQ and PR with a common vertex, then QS is parallel to PR, and RS is parallel to PQ (so the point in $\Bbb R^2$ we obtain from:

$P = (x_1,y_1)$
$Q = (x_2,y_2)$

so that $PQ = (x_2 - x_1,y_2-y_1)$

is the same point we obtain from:

(setting $R = (x_3,y_3), S = (x_4,y_4)$)

$RS = (x_4 - x_3,y_4 - y_3)$.

There are 3 possibilities for choosing the common vertex, we might choose P, Q, or R.

I will show you the point we get by choosing P as the common vertex, with the following assignments:

P = (1,1)
Q = (4,2)
R = (1,3)

then:

PQ = (4,2) - (1,1) = (3,1)
PR = (1,3) - (1,1) = (0,2)

If we set S = (a,b), then we want:

QS = (a,b) - (4,2) = (0,2) so (a,b) = (4,4).

To check that this makes sense, we verify that:

RS = (4,4) - (1,3) = (3,1) = PR.

You should be easily able to determine the other 2 possible "4th points".

In 3 or more dimensions, we get a "parallelpiped" (a cube is just a "regular orthogonal parallelpiped", and a "box" is an orthogonal parallelpiped).

If one thinks in terms of "coordinates", then the parallelpided spanned by the 3 vectors u,v and w is the "unit cube" in that coordinate system (which may not look like a cube at all in "standard coordinates"). One can think of the change of coordinates from standard to the u,v,w-system as being a kind of "distortion" that preserves lines.

 

[esis]

Thanks Deveno!

Ok, so since I had P, R and Q to start with, I should get two more parallelograms by adding two points a and b to P and R, and c and d to P and Q

PRab
a = R - RS = (1, 3) - (3, 1) = (-2, 2)
b = P - RS = (1, 1) - (3, 1) = (-2, 0)

PQdc
c = P - PR = (1, 1) - ((1, 3) - (1, 1)) = (1, 1) - (0, 2) = (1, -1)
d = Q - PR = (4, 2) - (0, 2) = (4, 0)

Illustrated, we would get:
View attachment 1929

Note that no parallelogram involving R and S is necessary in the task, as we did not have S to begin with.

However, I was also thinking about ways of producing lines, planes, and cubes using just a starting point and a specified R dimension using an algorithm instead of an algebraic solution. Limiting myself to vectors with length = 1:

View attachment 1930

During these last hours, I've started to think of them as walks (as in walks through a networked matrice graph consisting of vertices and arcs).

But then I again, this is just me playing around with ideas which are probably wrong. Nonetheless, I am learning stuff! I wonder if I could program a loop that did this for any specified dimension? Hmm. I think I'll get back to following the book for tomorrow, and see what happens next.

 

[Jameson]

Hi esis.
Just a little tip for attaching images. If you click on this icon View attachment 1928 and upload an image it won't repeat itself at the bottom of your post. :)

EDIT: Also, there was an issue with this uploader that made it difficult to attach more than one image. Maybe that's what happened to you. I believe I just applied a patch to fix this problem. Will test... yep, it works!

 

[esis]

Hi esis.
Just a little tip for attaching images. If you click on this icon https://www.physicsforums.com/attachments/1928 and upload an image it won't repeat itself at the bottom of your post. :)

Thanks! I was wondering about that. :)