Algorithm for Heap Insertion to Make New Node Rightmost Leaf

[evinda]

Hello and merry Christmas! (Happy)

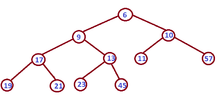
Suppose that we have this heap:

View attachment 3745

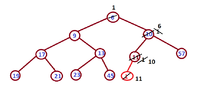
Applying this algorithm:

HeapInsert(HeapTable A, int size, Key K, Type I) {
      if (size == N) then error; /* Heap is full */
      m = size; 
      while (m > 0 and K < Α[floor((m-1)/2)]->Key) { 
               Α[m]->key = Α[floor((m-1)/2)]->Key; 
               Α[m]->data = Α[floor((m-1)/2)]->data; /
      }
      Α[m]->Key = K;
      Α[m]->data = I;
      size++;
}

we will get the following:

View attachment 3746

I want to rewrite the function [m]HeapInsert[/m] so that it is conducted from top to bottom. Especially, the function should make appropriate swaps of keys while traversing nodes from the root to the node that will be the parent node of the new inserted node.
These actions should be done so that after the insertion, the new inserted node is the rightmost leaf and that no further actions( for example swaps) are needed after the placement of the new node at the array that implements the heap. The function should have time complexity $O(\log m)$ and it should keep the properties of a heap.
So, do we have to create a new node that is the rightmost child of the last node of the second last level and then compare its key with the key of its parent node and if it is smaller to swap their values and continue this procedure till we find a key that is smaller or until we reach the root? (Thinking)

 

[Future Bruno]

Yes, that is one way of rewriting the HeapInsert function. You would have to traverse down the heap (from the root node to the node that will be the parent of the new inserted node) and compare the key of each node to the key of its parent. If the key of the node is smaller than the key of its parent, you would have to swap their values. By following this approach, you will ensure that the new inserted node is the rightmost child of the last node of the second last level and no further actions are needed after the placement of the new node at the array that implements the heap. This approach will have a time complexity of $O(\log m)$ and the properties of a heap will still be preserved.