mathhabibi
- 48
- 13
- TL;DR Summary
- Harmonic numbers, the digamma function, and a ton of special functions usually get a lot of attention, but no one cares about Alternating Harmonic Numbers. This post is intended to give them some love.
(Disclaimer: I don't know whether this type of post encouraging discussion on a function is allowed, if not please close this)
Hello PF,
If you're a fan of integrating, you'll hit a ton of special functions on the way. Things like the Harmonic Numbers, Digamma function, Exponential Integral, and things like that. One function that seldom appears in integrals (which results in it being largely forgotten) is the Alternating Harmonic Numbers. They are defined as $$\bar{H}_n=\sum_{k=1}^n\frac{(-1)^{k+1}}k$$ Clearly we have ##\lim_{n\rightarrow\infty}\bar{H}_n=\ln2## which is probably the only thing you know about it. Remember that ##n## can only be an integer. If we can extend ##\bar{H}_n##'s domain then we might be able to find some properties. How do we do it, you ask? Well, we will need a little trick. If we can turn the definition of ##\bar{H}_n## into an infinite series by continually adding and subtracting terms (i.e. make an infinite series that telescopes to ##\bar{H}_n##), then ##n## will no longer be in the upper bound and ##\bar{H}_n## would have a bigger domain. This telescoping series turns out to be $$\bar{H}_x=\sum_{k=1}^\infty\left(\frac{(-1)^{k+1}}k-\frac{(-1)^{k+1+x}}{k+x}\right)$$Note that we changed ##n## to ##x## because soon enough ##x## won't need to be an integer. I say soon enough because there is a ##(-1)^x## in the second fraction still forces ##x## to be an integer, but we can replace ##(-1)^x=\cos(\pi x)## and sum the first fraction to get $$\bar{H}_x=\ln2-\cos(\pi x)\sum_{k=1}^\infty\frac{(-1)^{k+1}}{k+x}$$We can stop here because now ##x## can be any real number except the negative integers. The infinite series can be rewritten, but before doing that, let's make a few observations. Notice how letting ##x=k+\frac12## for some ##k\in\mathbb{Z}## results in ##\bar{H}_x=\ln2##. Another thing is that, if we take the derivative of ##\bar{H}_x## with respect to ##x## and then let it be equal to ##0##, then we get that ##\bar{H}_0'=\frac{\pi^2}{12}##. This seems cool and all, but ##H_0'=\frac{\pi^2}6##, where ##H_x## represents the harmonic numbers, defined similarly like ##\bar{H}_x## but without the alternating symbol. One more thing we should talk about before rewriting the infinite sum is the roots of ##\bar{H}_x##. This is only a graphical observation, but take a look at this graph and focus on the three digits after the decimal point:
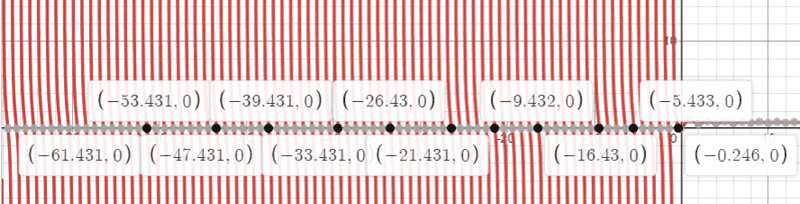
Notice here that, after many roots, the fractional part seems to approach ##-0.431##. I have no clue why this is true, but here's an interesting coincidence: $$\int_0^1\frac{\bar{H}_x\bar{H}_{-x}\sin(\pi x)}{\pi x}dx\approx0.431415917919$$The inspiration behind multiplying the sine function divided by ##\pi x## is because this is another way of writing ##\frac1{\Gamma(1-x)\Gamma(1+x)}## which removes the poles of ##\bar{H}_x\bar{H}_{-x}##. Notice here that, not only are the first three decimal digits 431, but there is a 314159 inside the decimal string, giving five accurate decimal digits of ##\pi##. This is most likely a coincidence because the ##1## after the last ##\pi## digit is fixed as the lower bound goes to ##0##. Now you might wonder why the lower bound wasn't equal to zero, and this is because of how I rewrote the infinite sum. So here it is: $$\sum_{k=1}^\infty\frac{(-1)^k}{k+x}=\psi(x)-\psi\left(\frac x2\right)-\frac1x-\ln2$$Where ##\psi## is the digamma function. When I have time I will write the proof of this in a different post (it's a little long). The important thing about this is that we can derive a reflection formula for ##\bar{H}_x## :$$\bar{H}_x-\bar{H}_{2-x}=\pi\cot(\pi x)-\left(\frac1{2-x}-\frac1{1-x}-\frac1x\right)\cos(\pi x)$$No special functions involved. Notice that the first term of the RHS is the reflection formula for the Digamma function. Also note that ##\psi(0)## is undefined, so I had to make the lower bound approach ##0## instead.
One more thing about ##\bar{H}_x## is that using the Euler-Maclaurin expansion to make a domain extension isn't that great because the integral involved will have to cross the singularities of ##\frac{\cos (\pi x)}{t+x}##, which are infinitely many, making it defined only when ##x>-1##. The analytic continuation by simply rewriting ##\bar{H}_x## as a telescoping series doesn't have this issue.
If you have anything else about the Alternating Harmonic Numbers, post them here! This function is very underrated so please spread the word :)
Hello PF,
If you're a fan of integrating, you'll hit a ton of special functions on the way. Things like the Harmonic Numbers, Digamma function, Exponential Integral, and things like that. One function that seldom appears in integrals (which results in it being largely forgotten) is the Alternating Harmonic Numbers. They are defined as $$\bar{H}_n=\sum_{k=1}^n\frac{(-1)^{k+1}}k$$ Clearly we have ##\lim_{n\rightarrow\infty}\bar{H}_n=\ln2## which is probably the only thing you know about it. Remember that ##n## can only be an integer. If we can extend ##\bar{H}_n##'s domain then we might be able to find some properties. How do we do it, you ask? Well, we will need a little trick. If we can turn the definition of ##\bar{H}_n## into an infinite series by continually adding and subtracting terms (i.e. make an infinite series that telescopes to ##\bar{H}_n##), then ##n## will no longer be in the upper bound and ##\bar{H}_n## would have a bigger domain. This telescoping series turns out to be $$\bar{H}_x=\sum_{k=1}^\infty\left(\frac{(-1)^{k+1}}k-\frac{(-1)^{k+1+x}}{k+x}\right)$$Note that we changed ##n## to ##x## because soon enough ##x## won't need to be an integer. I say soon enough because there is a ##(-1)^x## in the second fraction still forces ##x## to be an integer, but we can replace ##(-1)^x=\cos(\pi x)## and sum the first fraction to get $$\bar{H}_x=\ln2-\cos(\pi x)\sum_{k=1}^\infty\frac{(-1)^{k+1}}{k+x}$$We can stop here because now ##x## can be any real number except the negative integers. The infinite series can be rewritten, but before doing that, let's make a few observations. Notice how letting ##x=k+\frac12## for some ##k\in\mathbb{Z}## results in ##\bar{H}_x=\ln2##. Another thing is that, if we take the derivative of ##\bar{H}_x## with respect to ##x## and then let it be equal to ##0##, then we get that ##\bar{H}_0'=\frac{\pi^2}{12}##. This seems cool and all, but ##H_0'=\frac{\pi^2}6##, where ##H_x## represents the harmonic numbers, defined similarly like ##\bar{H}_x## but without the alternating symbol. One more thing we should talk about before rewriting the infinite sum is the roots of ##\bar{H}_x##. This is only a graphical observation, but take a look at this graph and focus on the three digits after the decimal point:
Notice here that, after many roots, the fractional part seems to approach ##-0.431##. I have no clue why this is true, but here's an interesting coincidence: $$\int_0^1\frac{\bar{H}_x\bar{H}_{-x}\sin(\pi x)}{\pi x}dx\approx0.431415917919$$The inspiration behind multiplying the sine function divided by ##\pi x## is because this is another way of writing ##\frac1{\Gamma(1-x)\Gamma(1+x)}## which removes the poles of ##\bar{H}_x\bar{H}_{-x}##. Notice here that, not only are the first three decimal digits 431, but there is a 314159 inside the decimal string, giving five accurate decimal digits of ##\pi##. This is most likely a coincidence because the ##1## after the last ##\pi## digit is fixed as the lower bound goes to ##0##. Now you might wonder why the lower bound wasn't equal to zero, and this is because of how I rewrote the infinite sum. So here it is: $$\sum_{k=1}^\infty\frac{(-1)^k}{k+x}=\psi(x)-\psi\left(\frac x2\right)-\frac1x-\ln2$$Where ##\psi## is the digamma function. When I have time I will write the proof of this in a different post (it's a little long). The important thing about this is that we can derive a reflection formula for ##\bar{H}_x## :$$\bar{H}_x-\bar{H}_{2-x}=\pi\cot(\pi x)-\left(\frac1{2-x}-\frac1{1-x}-\frac1x\right)\cos(\pi x)$$No special functions involved. Notice that the first term of the RHS is the reflection formula for the Digamma function. Also note that ##\psi(0)## is undefined, so I had to make the lower bound approach ##0## instead.
One more thing about ##\bar{H}_x## is that using the Euler-Maclaurin expansion to make a domain extension isn't that great because the integral involved will have to cross the singularities of ##\frac{\cos (\pi x)}{t+x}##, which are infinitely many, making it defined only when ##x>-1##. The analytic continuation by simply rewriting ##\bar{H}_x## as a telescoping series doesn't have this issue.
If you have anything else about the Alternating Harmonic Numbers, post them here! This function is very underrated so please spread the word :)