- #1
kenneth_G
- 1
- 0
Hello all!
New to the forums, and I have a question for you. In my classes, we have been dealing a lot with proofs lately, so when I was working on an assignment, I figured I would try and find my own proof for something, just for the hell of it. I decided to tacle the area of a right angled triangle, because I was using it in one of my assignments, and I wanted to skip some of the legwork I had to do to find the area. On my third try of finding a proof, I finally arrived at something useful.
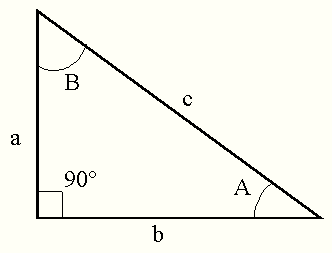
Starting with Area=½ab, I ended up with:
I verified my findings by comparing the results with the ½ab version, and they match. I also wanted to doube check it with some trusted source (and that I wasn't just getting lucky), so I searched around on the web, but can't find it listed anywhere.
So now the question: Has anyone seen this before? And where?
New to the forums, and I have a question for you. In my classes, we have been dealing a lot with proofs lately, so when I was working on an assignment, I figured I would try and find my own proof for something, just for the hell of it. I decided to tacle the area of a right angled triangle, because I was using it in one of my assignments, and I wanted to skip some of the legwork I had to do to find the area. On my third try of finding a proof, I finally arrived at something useful.
Starting with Area=½ab, I ended up with:
Area=¼ [itex]c^{2}[/itex]sin(2A)=¼ [itex]c^{2}[/itex]cos(2B)
I verified my findings by comparing the results with the ½ab version, and they match. I also wanted to doube check it with some trusted source (and that I wasn't just getting lucky), so I searched around on the web, but can't find it listed anywhere.
So now the question: Has anyone seen this before? And where?