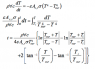- #1
SFAldabbous
- 1
- 0
Homework Statement
I need to find the temperature distribution for an aluminum sphere given that the heat radiated from the sphere is equal to the rate of change of internal energy.
Homework Equations
I couldn't understand the solution of the following integral.